КС. Движение по окружности

Движение по окружности

Период вращения — это время, за которое тело совершает один полный оборот.

• Обозначается буквой Т, измеряется в секундах (с).

Частота вращения — это величина, численно равная числу оборотов N, совершенных телом за время t = 1 с.

• Обозначается буквой ν, измеряется в герцах (1 Гц = 1с^–1).

Если тело за время t совершило N оборотов, то

$\begin{array}{c} {\nu =\dfrac{N}{t} ,\; \; \; T=\dfrac{t}{N} ,} \\ {} \\ {T=\dfrac{1}{\nu } ,\, \, \, \nu =\dfrac{1}{T} .} \end{array}$

Угол поворота (или угловое перемещение) — это угол, на который поворачивается радиус за некоторый промежуток времени t (рис. 1).

• Обозначается буквой φ, измеряется в радианах (1 рад).

• Не забывайте, что π = 3,14 рад = 180°.

Рис. 1

Пройденный путь тела при движении по окружности — это длина дуги окружности АВ (рис. 2).

• Обозначается буквой s, измеряется в метрах (м).

Рис. 2

Если тело за время t совершило N оборотов, то

$\begin{array}{c} {\varphi =2\pi \cdot N,\; \; \; s=2\pi \cdot R\cdot N,} \\ {} \\ {s=\varphi \cdot R.} \end{array}$

Угловая скорость — физическая величина, равная отношению угла поворота тела ω ко времени t, за которое этот поворот произошел:

$\omega =\dfrac{\varphi }{t} $.

• Обозначается буквой ω, измеряется радиан в секунду (рад/с).

Линейная скорость — физическая величина, равная отношению пройденного пути тела s ко времени t, за которое был пройденный этот путь:

$\upsilon =\dfrac{s}{t} .$

• Обозначается буквой υ, измеряется метр в секунду (м/с).

Если тело движется по окружности радиуса R, период вращения T, а частота вращения ν, то

$\begin{array}{c} {\upsilon =\omega \cdot R,} \\ {} \\ {\upsilon =\dfrac{2\pi \cdot R}{T} ,\; \; \; \upsilon =2\pi \cdot R\cdot \nu ,} \\ {} \\ {\omega =\dfrac{2\pi }{T} ,\; \; \; \omega =2\pi \cdot \nu .} \end{array}$

При движении по окружности линейная скорость $\vec{\upsilon }$ в любой точке направлена по касательной к траектории (перпендикулярно радиусу) (рис. 3).

Рис. 3

Так как направление линейной скорости постоянно меняется, то у тела должно быть ускорение, определяющее, как быстро меняется направление скорости. Такое ускорение называется центростремительным или нормальным (перпендикулярным).

• Обозначается а_ц, измеряется метр в секунду за секунду (м/с²).

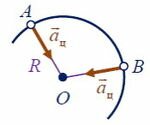
При движении по окружности радиуса R центростремительное ускорение $\vec{a}_{ц} $ направлено к центру окружности (по радиусу) (рис. 4) и равно

$a_{ц} =\dfrac{\upsilon ^{2} }{R} ,\; \; \; a_{ц} =\omega ^{2} \cdot R.$

Рис. 4