КС. Графики
Графики при прямолинейном движении
Равномерное движение
- График функции $y = b$ — прямая линия, перпендикулярная оси Y, где b — число.
- тело 1 движется по оси 0Х (υx > 0);
- тело 2 стоит на месте (υx = 0);
- тело 3 движется против оси 0Х (υx < 0).
Площадь заштрихованной фигуры численно равна пути, который проходит тело 1 за данный промежуток времени Δt = t1 – 0 = t1.
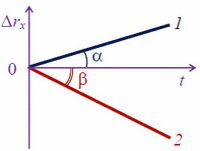
- График функции $y = b + k \cdot x$ — прямая линия, где b — число, k = tg α — это значение проекции скорости для графика проекции перемещения и координаты, α — угол наклона графика к оси 0Х.
- тело 1 равномерно движется по оси 0Х (Δrx > 0);
- тело 2 равномерно движется против оси 0Х (Δrx < 0).
- тело 1 равномерно движется по оси 0Х (координата x увеличивается);
- тело 2 неподвижно (координата x не изменяется);
- тело 3 равномерно движется против оси 0Х (координата x уменьшается).
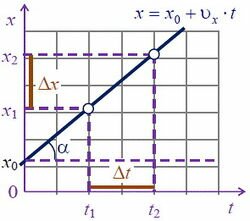
Для графика координаты $x=x_{0} +\upsilon _{0x} \cdot t$ проекция скорости равна $\upsilon _{x} ={\rm tg\; }\alpha =\dfrac{\Delta x}{\Delta t} =\dfrac{x_{2} -x_{1} }{t_{2} -t_{1} } $ (рис. 4), α — угол наклона графика к оси 0t, Δt = t2 – t1 — произвольный промежуток времени, x2 – x1 — промежуток координат, соответствующий промежутку времени Δt.
- Аналогично для графика проекции перемещения $\Delta r_{x} =\upsilon _{x} \cdot t$ находим проекцию скорости $\upsilon _{x}=\dfrac{\Delta r_{x2} -\Delta r_{x1} }{t_{2} -t_{1}}.$
Равноускоренное движение
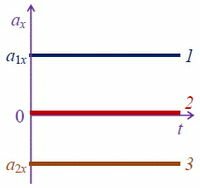
- График функции $y=b$ — прямая линия, перпендикулярная оси Y, где b — число.
- ускорение тела 1 направлено по оси 0Х (ax > 0);
- тело 2 движется равномерно (ax = 0);
- ускорение тела 3 направлено против оси 0Х (ax < 0).
- График функции $y=b+k\cdot x$ — прямая линия, где b — число, k = tg α — это значение проекции ускорения для графика проекции скорости, α — угол наклона графика к оси 0Х.
- тело 1 движется по оси 0Х с увеличением скорости (υx > 0, значение скорости увеличивается);
- тело 2 до точки А движется по оси 0Х с уменьшением скорости (υx > 0, значение скорости уменьшается), после точки А движется против оси 0Х с увеличением скорости (υx < 0, значение скорости увеличивается).
- Проекция перемещения тела 1 за промежуток времени Δt = t2 – t1 численно равна площади заштрихованной трапеции.
Для графика функции $\upsilon _{x} =\upsilon _{0x} +a_{x} \cdot t$ проекция ускорения $a_{x} =tg\, \alpha =\dfrac{\Delta \upsilon _{x} }{\Delta t} =\dfrac{\upsilon _{2x} -\upsilon _{1x} }{t_{2} -t_{1} } $ (рис. 7), где α — угол наклона графика к оси 0t, Δt = t2 – t1 — произвольный промежуток времени, Δυ = υ2 – υ1 — промежуток скоростей, соответствующий промежутку времени Δt.
- График функции $y=a+b\cdot x+c\cdot x^{2} $ — парабола, где a, b и c — число. Значение мгновенной скорости на графике проекции перемещения и координаты определяет тангенс угла наклона касательной в данный момент времени.
- тело 1 движется с увеличением значения скорости с ненулевой начальной скоростью (угол наклона касательной при t = 0 не равен нулю, и в дальнейшем угол наклона касательной увеличивается);
- тело 2 движется с увеличением значения скорости без начальной скорости (угол наклона касательной при t = 0 равен нулю, и в дальнейшем угол наклона касательной увеличивается);
- тело 3 движется с уменьшением значения скорости с ненулевой начальной скоростью (угол наклона касательной при t = 0 не равен нулю, и в дальнейшем угол наклона касательной уменьшается). В точке С тело останавливается, а затем начинает двигаться против оси 0Х с увеличением скорости.
- тело 4 движется с увеличением значения скорости с ненулевой начальной скоростью (угол наклона касательной при t = 0 не равен нулю, и в дальнейшем угол наклона касательной увеличивается);
- тело 5 движется с увеличением значения скорости без начальной скорости (угол наклона касательной при t = 0 равен нулю, и в дальнейшем угол наклона касательной увеличивается);
- тело 6 движется с уменьшением значения скорости с ненулевой начальной скоростью (угол наклона касательной при t = 0 не равен нулю, и в дальнейшем угол наклона касательной уменьшается). В точке С тело останавливается, а затем начинает двигаться по оси 0Х с увеличением скорости.
Вид графика координаты тела отличается от графика перемещения только смещением по вертикальной оси на x0. Например, тело 1 движется с увеличением значения скорости с ненулевой начальной скоростью (угол наклона касательной при t = 0 не равен нулю, и в дальнейшем угол наклона касательной увеличивается). Точно также будут двигаться тела 2 и 3, но
- тело 1 начало движение из точки x0 = 0;
- тело 2 начало движение из точки x0 > 0;
- тело 3 начало движение из точки x0 < 0.
- Аналогично будет меняться вид графика и для всех остальных тел (см. рис. 8, 9).
Обратите внимание, что:
- мгновенная скорость υх в вершине параболы графика Δrx(t) или x(t) (например, точка С на рис. 8 и 9) равна нулю;
- если тело вначале двигалось по оси 0Х (υx > 0), а затем против оси (υx < 0), то парабола расположена ветвями вниз (парабола 3 на рис. 8);
- если тело вначале двигалось против оси 0Х (υx < 0), а затем по оси (υx > 0), то парабола расположена ветвями вверх (парабола 6 на рис. 9).
Геометрический смысл мгновенной скорости (как производной координаты x): значение проекции мгновенной скорости υх в точке С графика x(t) равно тангенсу угла наклона α касательной к графику в точке С (рис. 11, а).
Точно построить касательную к параболе в произвольной точке С не совсем просто, а тем более затем еще определить угол ее наклона. Поэтому вместо касательной используют такую секущую АВ [1], что точка С лежит посередине между точками А и В (t3 – t1 = t1 – t2) (рис. 11, б). Тогда
- проекция мгновенной скорости в точке С равна $\upsilon _{x} =tg\, \beta =\dfrac{\Delta x}{\Delta t} =\dfrac{x_{3} -x_{2} }{t_{3} -t_{2} } ,$ где β — угол наклона секущей AB, Δt = t3 – t2 — промежуток времени, Δx = x3 – x2 — промежуток координат, соответствующий промежутку времени Δt.
- Чем меньше длина секущей АВ, тем ближе значение угла β к значению угла α, т.е. точнее значение мгновенной скорости.
- Аналогично для графика проекции перемещения Δrx(t) находим проекцию мгновенной скорости $\upsilon _{x} =\dfrac{\Delta r_{x2} -\Delta r_{x1}}{t_{2} -t_{1} } .$
Ссылки
- ↑ Секущая графика — это прямая AB, проведенную через любые две точки А и В графика функции x(t)
План построения графиков
- Проанализируйте функцию.
- Постройте таблицу значений данной функции и заполните ее.
- Постройте систему координат, выберите масштаб.
- Отметьте полученные точки и соедините их плавной линией.
Правила построения графиков
- Графики строят на бумаге с миллиметровой или другой специальной сеткой. Размер бумаги определяется интервалом изменения измеряемых величин и выбранным для них масштабом (но не наоборот!).
- По оси ординат (вертикальной) откладывают значения функции, по оси абсцисс (горизонтальной) — аргумента.
- На каждой из осей приводят только тот интервал изменения соответствующей физической величины, в котором велось исследование. Совсем не обязательно, чтобы на графике помещалось начало координат, т.е. точка (0, 0). На осях указывают обозначения и через запятую единицы соответствующих физических величин. Обозначения не следует наносить на поле, отведенное для графика. В случае очень больших или очень малых величин множители, определяющие порядок чисел, рекомендуется учитывать при обозначении.
- Масштаб графика выбирают не произвольно и не по размеру имеющегося кусочка миллиметровой бумаги. Он определяется абсолютными погрешностями тех величин, которые откладываются по осям. Погрешность каждой из величин должна представляться в выбранном масштабе отрезком заметной длины. Масштабы по каждой из осей выбирают независимо друг от друга. Оптимальным по точности для обеих осей одновременно будет наклон основной части кривой под углом, близким к 45°.
- Точки на график обводят кружком, при нескольких кривых используются различные фигуры: треугольники, квадратики и т.п.
- Кривую по нанесенным точкам проводят от руки плавно, без изломов и перегибов, а прямую — с помощью линейки. Линия графика не должна маскировать точек, поэтому она внутри фигурок, окружающих точки, не проводится.
- Любая особенность (максимум, минимум, перегиб, излом, резкое изменение кривизны и т.п.) на графике должна быть тщательно обоснована. В соответствующей области необходима большая густота экспериментальных точек, т.к. при малой густоте точек правильно провести график невозможно.
- Если на одном графике строят несколько кривых, то для их разделения используют различные линии: сплошные, пунктирные и т. д. Можно использовать различные цвета, цифровые, буквенные или другие обозначения.
Кембровский Г.С. Приближенные вычисления, методы обработки результатов изме-рений и оценки погрешностей в физике. — Мн.: ООО «Оракул», 1997. — С. 104-108.