SA. Сила Ампера

Материал из PhysBook

Сила Ампера

Действие магнитного поля на проводник с током исследовал экспериментально Андре Мари Ампер (1820 г.). Меняя форму проводников и их расположение в магнитном поле, Ампер сумел определить силу, действующую на отдельный участок проводника с током (элемент тока). В его честь эту силу назвали силой Ампера.

• Сила Ампера — это сила, с которой магнитное поле действует на помещенный в него проводник с током.

Согласно экспериментальным данным модуль силы F:

пропорционален длине проводника l, находящегося в магнитном поле;

пропорционален модулю индукции магнитного поля B;

пропорционален силу тока в проводнике I;

зависит от ориентации проводника в магнитном поле, т.е. от угла α между направлением тока и вектора индукции магнитного поля .

Тогда:

модуль силы Ампера равен произведению модуля индукции магнитного поля B, в котором находится проводник с током, длины этого проводника l, силы тока I в нем и синуса угла между направлениями тока и вектора индукции магнитного поля

,

• Этой формулой можно пользоваться:

  если длина проводника такая, что индукция во всех точках проводника может считаться одинаковой;

  если магнитное поле однородное (тогда длина проводника может быть любой, но при этом проводник целиком должен находиться в поле).

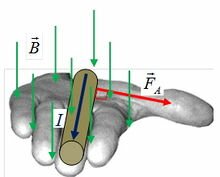
Для определения направления силы Ампера применяют правило левой руки: если ладонь левой руки расположить так, чтобы вектор индукции магнитного поля () входил в ладонь, четыре вытянутых пальца указывали направление тока (I), тогда отогнутый на 90° большой палец укажет направление силы Ампера () (рис. 1, а, б).

а

б

Рис. 1

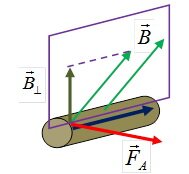
Поскольку величина B∙sin α представляет собой модуль компоненты вектора индукции, перпендикулярной проводнику с током, (рис. 2), то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к поверхности проводника должна входить в открытую ладонь левой руки.

Из (1) следует, что сила Ампера равна нулю, если проводник с током расположен вдоль линий магнитной индукции, и максимальна, если проводник перпендикулярен этим линиям.

Силы, действующие на проводник с током в магнитном поле, широко используются в технике. Электродвигатели и генераторы, устройства для записи звука в магнитофонах, телефоны и микрофоны — во всех этих и во множестве других приборов и устройств используется взаимодействие токов, токов и магнитов и т.д.

Сила Лоренца

Выражение для силы, с которой магнитное поле действует на движущийся заряд, впервые получил голландский физик Хендрик Антон Лоренц (1895 г.). В его честь эта сила называется силой Лоренца.

• Сила Лоренца — это сила, с которой магнитное поле действует на движущуюся в нем заряженную частицу.

Модуль силы Лоренца равен произведению модуля индукции магнитного поля , в котором находится заряженная частица, модуля заряда q этой частицы, ее скорости υ и синуса угла между направлениями скорости и вектора индукции магнитного поля

.

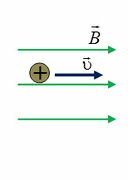
Для определения направления силы Лоренца применяют правило левой руки: если левую руку расположить так, чтобы вектор индукции магнитного поля () входил в ладонь, четыре вытянутых пальца указывали направления скорости движения положительно заряженной частицы (), тогда отогнутый на 90° большой палец укажет направление силы Лоренца () (рис. 3, а). Для отрицательной частицы четыре вытянутых пальца направляют против скорости движения частицы (рис. 3, б).

а

б

Рис. 3

Поскольку величина B∙sin α представляет собой модуль компоненты вектора индукции, перпендикулярной скорости заряженной частицы, , то ориентацию ладони можно определять именно этой компонентой — перпендикулярная составляющая к скорости заряженной частицы должна входить в открытую ладонь левой руки.

Так как сила Лоренца перпендикулярна вектору скорости частицы, то она не может изменить значение скорости, а изменяет только ее направление и, следовательно, не совершает работы.

Движение заряженной частицы в магнитном поле

1. Если скорость υ заряженной частицы массой m направлена вдоль вектора индукции магнитного поля, то частица будет двигаться по прямой с постоянной скоростью (сила Лоренца F_L = 0, т.к. α = 0°) (рис. 4, а).

а

б

в

Рис. 4

2. Если скорость υ заряженной частицы массой m перпендикулярна вектору индукции магнитного поля, то частица будет двигаться по окружности радиуса R, плоскость которой перпендикулярна линиям индукции (рис. 4, б). Тогда 2-ой закон Ньютона можно записать в следующем виде:

,

где , , α = 90°, т.к. скорость частицы перпендикулярна вектору магнитной индукции.

Тогда

.

3. Если скорость υ заряженной частицы массой m направлена под углом α (0 < α < 90°) к вектору индукции магнитного поля, то частица будет двигаться по спирали радиуса R и шагом h (рис. 4, в).

Действие силы Лоренца широко используют в различных электротехнических устройствах:

1. электронно-лучевых трубках телевизоров и мониторов;
2. ускорителях заряженных частиц;
3. экспериментальных установках для осуществления управляемой термоядерной;
4. МГД-генераторах

и т.д.

Литература

1. Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 321-322, 324-327.
2. Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 157-164.