О диоптре
По страницам сочинения Герона Александрийского «О диоптре» //Квант. — 2010. — № 3. — С. 23-25
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Герон александрийский творил на рубеже новой эры (предположительно I в. до н.э. - I в. н.э.). У своих современников он снискал славу искусного изобретателя. Телеги со специальным устройством Герона, послужившим прототипом современного таксометра, хорошо измеряли расстояние между городами и весями. Водяные часы Герона довольно точно отсчитывали время, синхронизируя события. Его храмовые автоматы по продаже «священной» воды безукоризненно отмеряли нужные порции. Насосы Герона качали воду, подпитывали фонтаны, а пневматические устройства закрывали и открывали двери перед изумленной публикой. Герон был непревзойденным знатоком всевозможных автоматических устройств и механических игрушек. Всего сказанного достаточно, чтобы понять, почему еще при жизни Герона, его, как и прославленного Архимеда (ок. 287-212 до н.э.), соотечественники уважительно величали: «Механик!»
Но Герон был не только прекрасным изобретателем, инженером, механиком, но и превосходным математиком. В его работе «Метрика» даны правила и формулы для вычисления площадей правильных многоугольников, объемов усеченных конуса и пирамиды, шарового сегмента, пяти правильных многогранников и даже тора. Современные школьники хорошо знают формулу Герона из его «Метрики», выражающую площадь треугольника S через длины трех его сторон a, b, c\[ S = \sqrt{p(p - a)(p - b)(p - c)} ,\] где \(p = \frac{a+b+c}{2}\) - полупериметр (эта формула была известна уже Архимеду). Однако не всякий школьник сможет без помощи калькулятора и таблиц рассчитать с высокой точностью значения таких корней, как \(\sqrt{2010}\ ,\ \sqrt[3]{2011}\ .\) Это безупречно умел делать Герон: в его «Метрике» мы находим описания эффективных вычислительных процедур для расчета квадратных и кубических корней со сколь угодно высокой точностью. Эти схемы вошли в арсенал инструментальных средств современной вычислительной математики.
В 1814 году обнаружилась находка, проливающая дополнительный свет на деятельность Герона: его сочинение «О диоптре». Некоторые комментаторы окрестили это сочинение «пособием по военному делу», увидев в диоптре «прибор для определения высоты стен фортификационных сооружений». Конечно же, скорлупу ореха можно разбивать любым твердым предметом, в том числе и волшебной палочкой, но эта палочка имеет и другие, не столь тривиальные применения. В золотых руках Герона диоптра превращается именно в «волшебный инструмент». В этом несложно убедиться, познакомившись с фантазиями Герона на тему диоптры, которые мы находим в его сочинении.
Мы приведем несколько фрагментов из сочинения Герона «О диоптре», основываясь на переводе этого труда видным специалистом по античной математике профессором И.Н.Веселовским. Расшифровку его рукописи, хранящейся в архиве ИИЕТ РАН, в «Фонде Веселовского», любезно предоставила доцент МИИТ Галина Александровна Зверкина. Здесь мы изложим фрагменты сочинения Герона в адаптированной форме, облегчающей понимание текста современным читателям.
Содержание
Что такое диоптра?
На рисунке 1 показана реконструкция диоптры, выполненная Г.Шене (Ф.Даннеман. История естествознания. - М.: Государственное медицинское издательство, 1932).
В верхней части прибора расположена круглая площадка, в плоскости которой вращается так называемая алидада - изогнутая на двух концах пластинка. С одной ее стороны в изогнутой части имеется точечное отверстие - глазной диоптр, а в другой щель с мушкой или тонким волоском - предметный диоптр. При рассмотрении через глазной диоптр мушка или волосок должны проектироваться на визируемую цель - это достигается вращением алидады в одной плоскости, которая, в свою очередь, также может поворачиваться с помощью специального регулирующего винта.
Диоптра позволяла с высокой точностью измерять углы как в вертикальной, так и в горизонтальной плоскости. Эти две незамысловатые возможности Герон виртуозно использовал для решения огромного множества задач, особо подчеркивая:
... все предложенные нами задачи практически разрешаются одним и тем же самыш [прибором]. Однако если кто-нибудь придумал и какие-нибудь другие [задачи], то устроенная нами диоптра не откажется разрешить и их. (Герон. О диоптре, I/Пер. И.Н. Веселовского.)
Недосягаемое становится доступным
Даны две точки, из которые одна вблизи нас, другая же вдали, найти между ними расстояние, не приближаясь к дальней точке. (Там же, VIII.)
На эту задачу, как на типовую, Герон неоднократно ссылается в дальнейшем. Для удобства ссылок назовем ее «Задача 1».
Пусть от точки А требуется найти расстояние до недоступной точки K.
С помощью диоптры отмечается точка В на прямой КА, и под прямым углом к прямой АК проводятся отрезки \(AC \perp AK \ ,\ BD \perp BK\) так, что точки К, С, D располагаются на прямой линии (рис. 2).
Поскольку треугольники DBK и CAK подобны, то справедлива пропорция \(\frac{BD}{AC} = \frac{BK}{AK}\) . Длины отрезков АС, BD, AB измеряются непосредственно, а длина отрезка AK находится из этой пропорции.
Точка K может быть кораблем в море, камнем на другом берегу реки, вершиной египетской пирамиды - все эти недоступные для непосредственного измерения объекты способ Герона превращает в доступные.
Далеко ли разошлись корабли?
Для двух недоступных точек определить расстояние между ними. (Там же, X.)
Герон предлагает несколько способов решения этой задачи. Рассмотрим один из них. Определив по способу задачи 1 расстояния от точки А до двух недоступных точек К и F, откладываем какую-нибудь часть этих расстояний на продолжении прямых КА и FA (рис.3). Получаем доступный измерению треугольник АСВ, подобный треугольнику AFK. Длина отрезка СВ составляет известную часть от длины отрезка KF, что и позволяет его найти.
Как высоко дерево?
Определить высоту недоступного дерева. (Там же, XII.)
В решении этой задачи, кроме диоптры высоты d, используется также вспомогательный шест высоты h. Пусть удаление диоптры от дерева равно L (его можно определить по способу, изложенному в задаче 1), а шест отстоит от диоптры на расстоянии l. Визируется верхушка дерева неизвестной высоты H, как показано на рисунке 4. Поскольку прямоугольные треугольники: больший с катетами L и H - h и меньший с катетами I и h - d подобны, то справедлива пропорция \(\frac{H - d}{L} = \frac{h - d}{l}\) откуда определяется H.
Точно такая же пропорция будет иметь место, если L и I обозначают не катеты, а известные гипотенузы - в этом случае можно найти, например, недоступную высоту пирамиды H (рис. 5).
Расстояние до невидимой точки
От данной точки к другой точке, являющейся невидимой, провести при помощи диоптры прямую, каково бы ни было расстояние между ними. (Там же, VII.)
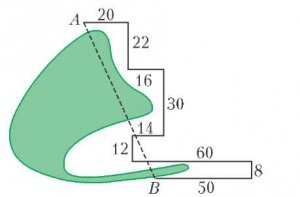
Пусть точки А и В загорожены друг от друга лесным массивом и не находятся на линии прямой видимости (рис.6). С помощью диоптры проведена вспомогательная ломанная линия, соседние звенья которой расположены под прямым углом друг к другу. Измеренные расстояния вдоль звеньев указаны на рисунке. Определите по этим данным расстояние между точками А и В самостоятельно.
Площадь недоступного объекта
Измерить данную площадь, не входя на эту площадь или вследствие обилия растительности, или помехи от зданий, или от того, что не допускается в нее входить. (Там же, XXVII.)
Пусть недоступный объект, площадь которого следует определить, задан своим контуром, например выпуклым многоугольником ABCDEF (рис. 7). Мысленно разобьем его на треугольники с общей вершиной А и последовательно определим площадь каждого из них, начиная с треугольника AEF.
Отложим на продолжении стороны AF какую-нибудь ее часть FH, а на продолжении стороны EF - такую же ее часть FG. Тогда треугольник HFG будет подобен треугольнику AFE. Умножив отрезок HG на коэффициент подобия, узнаем величину недоступного отрезка EA, а умножив площадь треугольника HFG на квадрат коэффициента подобия, найдем площадь недоступного треугольника AFE.
Решение этой задачи Герон заканчивает такой фразой:
Подобно же определим и содержание каждого из остальных треугольников; таким образом возможно определить содержание и всей площади. (Там же, XXVII.)
В сочинении Герона разбираются также и другие задачи, решаемые с помощью диоптры, например:
• взять глубину данного рва (XIV);
• прокопать по прямой [линии] гору при заданных на горе отверстиях туннеля (XV);
• к подземному ходу провести в горе шахту, перпендикулярную к ходу (XVI).
Некоторые историки науки полагают, что в сочинении Герона «О диоптре» изложены правила земельной съемки, фактически основанные на использовании прямоугольных координат.