Kvant. Эквивалентные деформации
Эпштеин В. Метод эквивалентных деформаций //Квант. — 2009. — № 1. — С. 40-41.
По специальной договоренности с редколлегией и редакцией журнала "Квант"
Математика представляет собой естественный язык, на котором формулируются и решаются физические задачи. И, тем не менее, для понимания элементарных (а может быть, и фундаментальных) оснований науки об окружающем нас мире полезно познакомиться с задачами, решение которых не требует проведения математических расчетов. Так, метод эквивалентных деформаций предполагает ряд мысленных изменений конфигурации (т.е. геометрических размеров и формы) тел, при которых основные характеристики системы остаются неизменными, но ход исследуемых процессов становится очевидным. Вашему вниманию предлагается несколько таких задач.
Задача 1.
В небольшом бассейне плавает лодка. Изменится ли (и если изменится, то как) уровень воды в бассейне, если лежащий на дне лодки камень бросить в воду?
Решение
Расчетные методы решения этой задачи предложены во многих учебных пособиях. Можно, однако, обойтись и без расчетов.
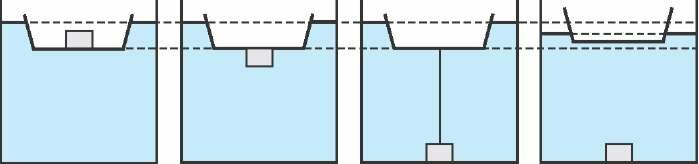
Подумаем: зависит ли ответ на вопрос, поставленный в задаче, от формы дна лодки, на котором лежит камень? Ясно, что такой зависимости быть не может: в законе Архимеда форма тела, погруженного в жидкость, никакой роли не играет. Тогда будем мысленно «продавливать» камень через дно лодки. Последовательные стадии этого процесса представлены на рисунке 1. На одном из этапов камень можно представить подвешенным на веревке, привязанной ко дну лодки. Уровень воды, естественно, не изменится, если удлинить веревку так, чтобы камень коснулся дна бассейна. Если же веревку теперь перерезать, то, очевидно, лодка всплывет, и, следовательно, уровень воды понизится.
Задача 2.
В стакане плавает кусок льда, содержащий: а) пузырёк, наполненный воздухом; б) кусочек пробки; в) стальную гайку. Как изменится уровень воды в стакане, когда лед растает?
Решение
Заметим для начала, что если лед однороден, то после его таяния уровень воды не изменится: лед вытесняет ровно столько воды, сколько сам весит и, следовательно, сколько получится при плавлении.
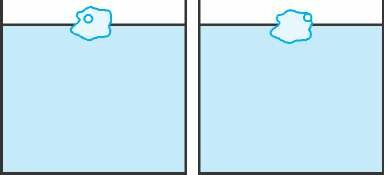
Ясно, что решение задачи не зависит от места расположения указанных объектов в куске льда. В случае а), к примеру, пузырек можно переместить к поверхности льда (рис.2). Таким образом, наличие пузырька эквивалентно изменению формы однородного льда, плавление которого, как уже говорилось, уровня воды не изменяет.
Следует отметить, что, строго говоря, сказанное выше справедливо лишь в том случае, если плотность влажного воздуха в пузырьке совпадает с плотностью окружающего атмосферного воздуха. В состоянии термодинамического равновесия это возможно только в так называемой тройной точке, т.е. при таких значениях температуры и давления, при которых лед, вода и водяной пар находятся в равновесии (\(~t \approx 0,01 ^\cdot C , p \approx ^\cdot 4,6 \)мм рт. ст).
Таяние льда с вмерзшей пробкой - случай б) - уровень воды не изменит, так как пробку можно мысленно выдавить изо льда и пустить в самостоятельное плавание на тонкой ледяной нити.
В случае в) гайку, как и в первой задаче, «продавим» сквозь лед до дна стакана, а затем перережем связывающую ледяную нить. Лед всплывет, уровень воды понизится и уже не изменится после плавления льда.
Задача 3.
Закрытый пробкой сосуд, вес которого равен выталкивающей силе, покоится на дне стакана с водой. Почти не совершая работы, его можно поднять к поверхности воды. Если теперь вынуть пробку, то сосуд наполнится водой и утонет. При этом он может совершить некоторую работу. Если же вынуть пробку, когда сосуд лежит на дне, он также наполнится водой, но работы не совершит. Как согласовать полученные результаты с законом сохранения энергии?
Решение
Обсудим, в чем суть парадокса.
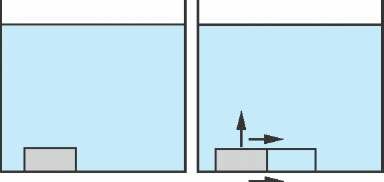
В первой части задачи речь идет о том, что при падении сосуда, заполненного водой, работа совершается несмотря на то, что для поднятия тела не пришлось затратить никакой энергии. Произведем, однако, с сосудом в исходном состоянии эквивалентную деформацию: мысленно деформируем лежащий на дне сосуд так, как показано на рисунке 3. «Выдавим» массу стенок в перемещенную часть, а пустую часть сосуда отделим от заполненной. Вода окажется «захваченной» стенками сосуда и, таким образом, будет находиться внутри сосуда. Теперь сосуд и «воздух» можно поднимать раздельно. Поднимая сосуд, мы совершаем работу. Поднятие «воздуха» эквивалентно опусканию некоторого объема воды (массы этой воды и сосуда равны). Ситуация совершенно аналогична повороту равно-плечного рычага с равными грузами на концах. Поднимая один груз, мы опускаем другой (рычаг находится в положении безразличного равновесия - работа не совершается). Затем мы можем перерезать нить, которой привязан поднятый груз. При падении этого груза сила тяжести совершит работу.
Применяя этот же метод во второй части задачи, мы не видим существенных различий с уже рассмотренным случаем. Наполнение водой сосуда эквивалентно перемещению известного объема воды от поверхности до дна стакана.
Работа при этом выполняется такая же, что и в первом случае (при перемещении сосуда).
Отличие условий первой части задачи от второй сводится, таким образом, всего лишь к порядку действий. Нарушения закона сохранения энергии не обнаруживается.
Задача 4.
Сосуд наполовину заполнен водой, в которой плавает кусок льда. Поверх льда наливают керосин, верхний уровень которого устанавливается на высоте h от дна сосуда. Как изменится эта высота, когда лед растает?
Решение
Эта задача была опубликована в «Задачнике «Кванта» (Ф113) в 1971 году. В журнале приведено строгое математическое решение этой (не очень сложной) задачи. Можно, однако, обойтись и без расчетов.
В случае, когда лед оказывается под поверхностью керосина, ответ очевиден: вода, полученная после плавления льда, занимает меньший объем, значит, верхний уровень керосина понизится.
Интерес представляет анализ ситуации, когда лед выступает над поверхностью керосина. Идея эквивалентных деформаций порождает соблазн деформировать лед так, чтобы его вершина оказалась под поверхностью керосина. Таким образом, казалось бы, можно свести рассматриваемую задачу к предыдущей. Однако этот «фокус» не проходит: погружение выступающей части льда в керосин сопровождается повышением уровня жидкости, а после плавления уровень понижается - следовательно, конечный результат не будет очевидным. Итак, деформация оказывается неэквивалентной.
Но если эквивалентная деформация льда не проходит, не стоит ли двинуться в противоположном направлении: оставить лед в покое, а «деформировать» жидкости? Попробуем.
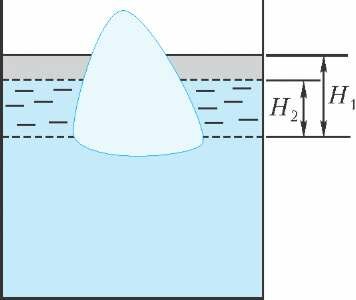
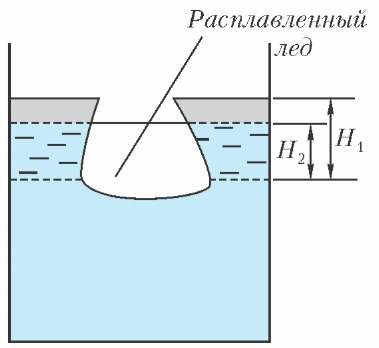
Для этого слой керосина толщиной H1 заменим таким слоем воды, который сохраняет положение льда неизменным (рис.4). Поскольку плотность воды больше плотности керосина, высота этого слоя H2 < H1. При плавлении льда уровень воды (как было замечено выше) не меняется. Если теперь осуществить обратную замену и вернуть на место керосин (для этого следует оставить след поверхности льда, как показано на рисунке 5), то выяснится, что слой керосина над поверхностью, которую ранее образовывала вода, растекается по большей площади и уровень керосина понижается (по сравнению с исходным).
Итак, уровень керосина понижается независимо от того, покрывает керосин ледяную глыбу полностью или частично. Несмотря на то, что эквивалентную деформацию льда осуществить не удалось, сама идея метода оказалась плодотворной.