Kvant. Сверхзвук

Стасенко А.Л. Как Студент на сверхзвук выходил //Квант. — 2000. — № 5. — С. 34-35.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Не делай ничего наугад, а только по правилам искусства.

Марк Аврелий

В ночь перед экзаменом по аэродинамике приснился Студенту страшный сон — будто, падая с кровати, достиг он сверхзвуковой скорости. Вскочив в холодном поту, задумался Студент: в самом деле, с какой высоты нужно упасть, чтобы достичь сверхзвука в атмосфере Земли? Вопрос не праздный - ведь этак можно было бы обойтись без аэродинамических труб, требующих большой мощности для разгона воздуха! И еще преимущество: поток воздуха в аэродинамической трубе неизбежно турбулентный (возмущенный), а в атмосфере турбулентность естественная, может быть, как раз такая, как в реальном полете. И еще важное соображение: исследуемое тело, например самолет или его модель, может быть любых размеров, в отличие от (поневоле) малых размеров в трубе. И еще... Но и перечисленных прелестей казалось достаточно, чтобы Студент с воодушевлением взялся за физические оценки.

Рис. 1

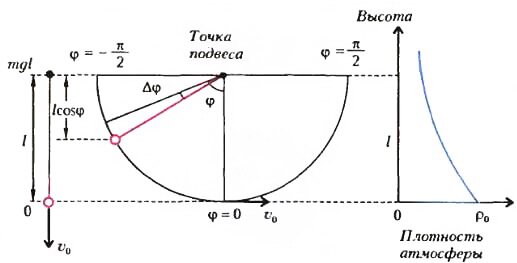
Еще в школе он знал, что тело, сброшенное с высоты l, достигает (в вакууме) скорости (рис.1, слева)

\(~\upsilon_0 = \sqrt{2gl}\) . (1)

Значит, чтобы достичь скорости порядка 330 м/с, высота должна быть равна

\(~l = \frac{\upsilon^2_0}{2g} = \frac{(3,3 \cdot 10^2)^2}{2 \cdot 10}\) м ≈ 5 км.

(Конечно, не обязательно падать вертикально: можно, привязав тело к нити длиной l, достичь той же скорости в нижней точке колебаний. Что гораздо лучше: опыт будет снова и снова повторяться, пока продолжаются колебания - в отличие от одноразового падения вниз.)

Но в вакууме никакого звука нет — значит, нет и понятия сверхзвукового движения. А воздух будет оказывать сопротивление движению, и качественно ясно, что начальная высота, падая с которой тело может достичь сверхзвуковой скорости, должна быть больше полученной выше оценки. И, значит, на таких масштабах плотность атмосферы ρ уже не придется считать постоянной величиной (см. рис.1, справа) - об этом отлично знают альпинисты.

Силу сопротивления можно описать, исходя из соображений размерностей:

\(~F = C \frac{\rho \upsilon^2}{2} S\) . (2)

Здесь \(~\frac{\rho \upsilon^2}{2}\) — так называемый скоростной напор (он имеет размерность давления), S - характерная площадь тела, например его лобового сечения. А вот С - это безразмерный коэффициент сопротивления, который теория размерностей, естественно, «не чувствует». Ради его измерения и построены во всем мире мощные аэродинамические трубы, ради него Студент и задумался.

Так возник Проект Экспериментальной Установки.

Возьмем невесомую нерастяжимую нить длиной l, подвесим на ней сверхзвуковой авиалайнер (например, ТУ-144) или истребитель массой m и, приведя этот «математический маятник» в горизонтальное положение, отпустим (см. рис. 1, в центре). Потенциальная энергия самолета в любой точке его траектории, характеризуемой углом φ, равна

\(~mgl(1 - \cos \varphi)\) .

Проверим: в начальной точке, когда \(~\varphi = -\frac{\pi}{2}\), соs φ = 0 и эта энергия равна mgl, а при φ = 0 (в самой нижней точке траектории) она равна нулю.

Не будь потерь энергии на сопротивление, суммарная механическая энергия сохранялась бы (собственно, из этого условия и найдена скорость υ₀ в формуле (1)):

\(~m \left(\frac{\upsilon^2}{2} + gl(1 - \cos \varphi ) \right) = mgl\) . (3)

Но если есть сила сопротивления, то суммарная механическая энергия колеблющегося тела будет убывать. Работа силы сопротивления на небольшом участке пути длиной lΔφ равна, очевидно, FlΔφ. Значит, учитывая выражения (2) и (3), можно записать

\(~\Delta \left(\frac{\upsilon^2}{2} + gl(1 - \cos \varphi ) \right) = -\frac{\upsilon^2}{2} \left( C\frac{\rho Sl}{m}\right) \Delta \varphi\) . (4)

Обозначим набор величин в правой части в скобках одной буквой:

\(~\beta = \frac{C \rho Sl}{m}\) .

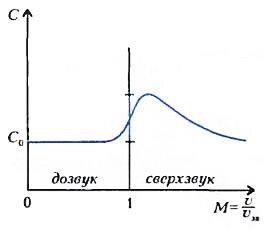
Вообще говоря, это не постоянная. Действительно, первая же оценка по формуле (1) показала, что проектируемое устройство будет циклопическим сооружением, поэтому плотность воздуха ρ будет заметно изменяться на таких масштабах. Да и безразмерный коэффициент сопротивления С не постоянен, а зависит от отношения скорости движения тела к скорости звука υ_zv, т.е. от числа Маха \(~M = \frac{\upsilon}{\upsilon_{zv}}\). Вблизи М = 1 он резко возрастает (рис.2), а затем уменьшается с ростом М (для чего и делаются стреловидные крылья у сверхзвуковых самолетов). Конечно, все это можно учесть в правой части уравнения (4) и, решив его, например численно на компьютере, сравнить результаты теории и эксперимента, из чего и будет получена информация об искомом коэффициенте сопротивления.

Рис. 2

Но Студент сделал проще. Чтобы оценить все-таки длину подвеса, при которой лайнер заведомо достигнет скорости звука, он сделал Оценку Сверху, или, как изящно выражаются математики, мажорировал. Для этого он выбрал для плотности самое большое значение ρ₀ ≈ 1 кг/м³ (у поверхности Земли), для коэффициента сопротивления взял максимальное значение (приблизительно вдвое большее, чем при дозвуковых скоростях) С ≈ 2C₀, а скорость в выражении для работы силы сопротивления решил мажорировать ее значением для случая вакуума, которое получается из выражения (3):

\(~(\upsilon^0)^2 = 2gl \cos \varphi = \upsilon^2_0 \cos \varphi\) .

Итак, в формуле (4) справа стоит убыль механической энергии, заведомо бблыпая (по модулю), чем в реальности, но зато теперь можно проще узнать, сколько будет «съедено» энергии, например на участке траектории от верхней точки (\(~\varphi = -\frac{\pi}{2}\)) до нижней (φ = 0). Для этого надо сложить все потери энергии на каждом малом Δφ, или, как говорят взрослые, проинтегрировать функцию

\(~-\beta_{max} \frac{\upsilon^2_0}{2} \cos \varphi\) ,

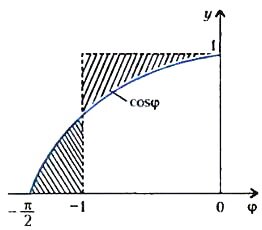
где, по договору, \(~\beta_{max} = \frac{2C_0 \rho_0 Sl}{m}\). При этом придется найти площадь под кривой y = соs φ (рис.3). Кто умеет, да возьмет интеграл:

\(~\int^0_{-\frac{\pi}{2}} \cos \varphi d \varphi = \sin \varphi |^0_{-\frac{\pi}{2}} = 0 - \sin \left( -\frac{\pi}{2} \right) = 1\) .

А кто не умеет, и так поймет, взглянув на рисунок 3, что эта площадь порядка единицы (там для наглядности заштрихованы участки одинаковой площади).

Рис. 3

Теперь изменение суммарной механической энергии можно записать так:

\(~\left(\frac{\upsilon^2}{2} + gl(1 - \cos 0) \right) - \left(0 + gl \left(1 - \cos \left( -\frac{\pi}{2} \right) \right) \right) = -\beta_{max} gl \cdot 1\) .

Потребуем, чтобы скорость тела в нижней точке (φ = 0) стала равной скорости звука: υ = υ_zv, и учтем, что cos 0 = 1, a \(~\cos \left( -\frac{\pi}{2} \right) = 0\). Тогда

\(~\left(\frac{\upsilon^2}{2} + 0 \right) - (0 + gl) = -\beta_{max} gl\) .

В результате получим квадратное уравнение для искомой длины l:

\(~\upsilon^2_{zv} = 2g (1 - \beta_{max}) l = 2g \left(1 - \frac{2C_0 \rho_0 Sl}{m} \right) l\) .

Подставляя характерные значения величин для «типичных» сверхзвуковых истребителей: m = 30 т, S = 50 м², C₀ = 0,01, найдем

l₁ ≈ 7 км и l₂ ≈ 20 км .

Даже меньший из этих двух корней сравним с высотой самых высоких гор на Земле.

И еще одна мысль пронзила Студента: центробежная сила!? Ведь вблизи нижней точки центростремительное ускорение будет равно

\(~\frac{\upsilon^2_{zv}}{l} \approx 1,5 g\) ,

значит, перегрузка составит 2,5g - лайнер «потяжелеет», и это надо учесть при выборе троса.

Таким образом, если пропилить в самой высокой горе пропасть с вертикальными стенками шириной в несколько размахов крыла, затем наверху установить горизонтальную ось вращения, подвесить лайнер на тросе длиной семь километров... - работы хватит всем и надолго. А кстати, где можно достать тонкую (желательно нерастяжимую) нить длиной несколько километров, способную выдержать вес нескольких авиалайнеров?

С этими мыслями Студент и пошел на экзамен по экспериментальной аэродинамике. Результат экзамена в летописях не сохранился...