Kvant. Геометрия тонкой линзы

Дроздов В. Геометрия тонкой линзы //Квант. — 1997. — № 2. — С. 29.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

Тонкой линзой называется линза, толщина которой h значительно меньше радиусов кривизны R₁ и R₂ ее сферических поверхностей. Именно для такой линзы выводится формула для определения ее фокусного расстояния F (попробуйте сделать это самостоятельно):

\(~\frac 1F = (n - 1) \left( \frac{1}{R_1} + \frac{1}{R_2} \right),\)

где n — показатель преломления стекла линзы. Однако, держа линзу в руках, трудно оценить на глаз радиусы кривизны R₁ и R₂, но легко определить толщину линзы h и ее диаметр d. Интересно сопоставить величины h и d в тонкой (по определению) линзе.

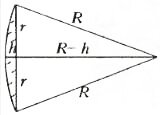
Для простоты вычислений рассмотрим плосковыпуклую линзу с радиусом кривизны сферической поверхности R. Геометрически такая линза представляет собой шаровой сегмент, изображенный на рисунке. Безразмерное отношение \(~\frac hR\) обозначим λ и учтем, что \(~\lambda \ll 1\). Согласно теореме Пифагора, запишем \(~R^2 = (R - h)^2 + r^2\), откуда имеем \(~r^2 = 2Rh - h^2 \approx 2R^2 \lambda\). Теперь найдем диаметр линзы: d = 2r и отношение \(~\frac hd\):

\(~\frac hd = \sqrt{\frac{\lambda}{8}}.\)

Видим, что при \(~\lambda \ll 1\) справедливо неравенство \(~\frac hd \ll 1\). (Так, при λ = 0,02 получим \(~\frac hd = 0,05\).) Значит, линза, тонкая по определению, будет тонкой и по зрительном восприятию.

Теперь займемся вычислением фокусного расстояния нашей линзы. С одной стороны, фокусное расстояние линзы, у которой R₁ = R и R₂ = ∞, равно \(~F = \frac{R}{n - 1}\). С другой стороны, как легко показать, справедливо равенство \(~R = \frac{d^2 + 4h^2}{8h}\). Отсюда получаем

\(~F = \frac{d^2 + 4h^2}{8(n - 1)h}.\)

Следовательно, если знать показатель преломления п стекла, из которого изготовлена линза, то можно определить величину F, просто обмерив линзу.