Kvant. Бесплатный полет

Стасенко А.Л. Как бесплатно улететь на каникулы //Квант. — 1997. — № 1. — С. 39-40.

По специальной договоренности с редколлегией и редакцией журнала "Квант"

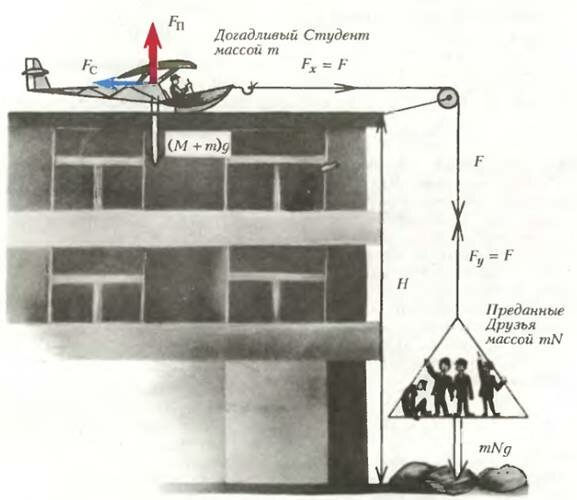
«Однажды в студеную зимнюю пору я из лесу вышел. Был сильный мороз. Гляжу...». Тут Догадливый Студент взглянул на высокое здание общежития — и его осенило. Он хотел домой на каникулы. Но авиабилеты были дороги, идти в ночные грузчики или в «комок» было неохота, а сила Знания безгранична. И осенила его Мысль. Если сделать планер и разогнать его вдоль скользкой оледеневшей крыши... А разогнать при помощи невесомого нерастяжимого троса, перекинутого через блок без трения, и при участии нескольких Преданных Друзей (рис.1). Да если при этом еще пренебречь трением о крышу и сопротивлением воздуха...

Рис. 1

Итак, пусть масса планера М, масса Догадливого Студента и каждого его Друга m, сила натяжения троса F. Тогда можно записать уравнения второго закона Ньютона для горизонтального движения планера с пилотом (масса М + m) и вертикального движения люльки с N Преданными Друзьями (масса mN, а люлька пусть невесома):

\(~\begin{matrix} (M + m)a_x = F_x \\ mNa_y = mNg - F_y \end{matrix}\) .

Но поскольку трос нерастяжим, модули ускорений его концов и ускоряющих сил одинаковы, т.е. a_x = a_y = a, F_x = F_y = F. Поэтому предыдущие равенства можно записать в виде одного уравнения (исключив F, как сказал бы математик)

\(~(M + m(N + 1))a = mNg\) . (1)

Смысл этого уравнения очевиден: справа стоит сила тяжести всех Преданных Друзей, а слева — масса всей системы (включая массу Догадливого Студента и его планера), которой упомянутая сила тяжести сообщает ускорение а.

Согласно уравнению (1), ускорение постоянно, значит, скорость будет расти со временем линейно, а пройденный путь — квадратично:

\(~\begin{matrix} \upsilon = at \\ s = y = a \frac{t^2}{2} \end{matrix}\) ,

где \(~a = \frac{mN}{M + m(N + 1)} g\) .

Но в рассматриваемой ситуации важно не время. Важно, чтобы высота общежития Н и число преданных Друзей N были достаточны для достижения какой-то наименьшей скорости υ_*, при которой можно будет взлететь. Поэтому, исключив время t, лучше записать зависимость скорости от пройденного пути в виде

\(~\upsilon = \sqrt{2ay}\) или \(~\frac{\upsilon^2}{2} = ay\). (2)

Последнее равенство уж очень что-то напоминает. Подставив сюда а, получим

\(~(M + m(N + 1))\frac{\upsilon^2}{2} = (mNg)y\) . (3)

Это — закон сохранения полной механической энергии: кинетическая энергия общей массы системы \(~M_0 = M + m(N + 1)\) приобретается за счет изменения потенциальной энергии Преданных Друзей при их опускании по вертикальной координате от 0 до -y или за счет работы постоянной силы mNg на пути s = y. И «энергетическое» утверждение (3) в отсутствие потерь механической энергии (что и предполагалось) адекватно «силовому» уравнению (1).

Рис. 2

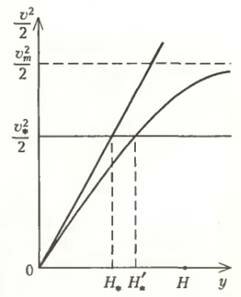
Итак, в принятых предположениях удельная кинетическая энергия системы \(~\frac{\upsilon^2}{2}\) (в расчете на единицу массы) пропорциональна расстоянию y (см. равенство (2) и рисунок 2). Но какую наименьшую скорость υ_* надо набрать при у = H? Очевидно, такую, при которой подъемная сила планера F_p станет равной силе тяжести (М + m)g. Из соображений размерностей, например, легко понять, что подъемная сила пропорциональна квадрату скорости, площади крыла S и плотности воздуха ρ :

\(~F_p \sim \frac{\upsilon^2}{2} S \rho\) . (4)

А чтобы знак пропорциональности заменить знаком равенства, нужно поставить в эту формулу еще какой-то безразмерный множитель С, который зависит от конструкции планера, но никак не «охватывается» теорией размерности. Для его определения нужны другие теории или эксперимент. Он так и называется: коэффициент сопротивления. Таким образом, чтобы взлететь, нужно соблюсти условие

\(~C\frac{\upsilon^2_*}{2} S \rho = (M + m)g\) . (5)

На рисунке 2 проведена горизонтальная прямая, соответствующая этой наименьшей скорости υ_*.

И тут Догадливого Студента осенила следующая мысль: как же так — подъемная сила есть, значит, воздух есть, а сопротивления воздуха нет?! Не может такого быть. Поэтому либо в уравнение (1) нужно добавить силу сопротивления воздуха F_c, либо в уравнение (3) — ее работу. По-видимому, сила сопротивления должна зависеть от тех же величин, что и подъемная сила (см. равенство (4)), только с каким-то другим безразмерным коэффициентом сопротивления C_x. Чем меньше сопротивление при данной подъемной силе, тем более совершенен летательный аппарат. Существует понятие аэродинамического качества летательного аппарата \(~K = \frac{C}{C_x}\), с помощью которого силу сопротивления планера можно записать в виде

\(~F_c = -\frac{F_p}{K} = -\frac{C}{K} \frac{\upsilon^2}{2} S \rho\) .

Добавим теперь работу этой силы в уравнение (3). Но поскольку эта сила изменяется по мере ускорения планера, уравнение нужно записывать не для конечного расстояния y, а для малых приращений Δy, внутри каждого из которых переменные силы можно считать постоянными:

\(~M_0 \Delta \left(\frac{\upsilon^2}{2}\right) = mNg \Delta y - \frac{C}{K} \frac{\upsilon^2}{2} S \rho \Delta y\) . (6)

Получилось так называемое дифференциальное уравнение относительно \(~\frac{\upsilon^2}{2}\) как функции y. Эти страшные слова не смутили Догадливого Студента. Уравнение простенькое, решать такие он умел еще в школе. Но многое можно сказать, даже не решая это уравнение.

Например, совершенно ясно, что в любой момент времени (или при любом значении y) скорость планера с учетом силы сопротивления будет меньше, чем без учета этой силы. Значит, соответствующая кривая на рисунке 2 пойдет ниже прямой ay. Далее, когда (из-за увеличения скорости) сила сопротивления станет равной постоянной силе тяжести mNg, скорость перестанет изменяться и достигнет предельного значения υ_m. Положив левую часть уравнения (6) равной нулю, получим

\(~\frac{\upsilon^2_m}{2} = mNg \frac{K}{CS \rho}\) . (7)

Эта горизонтальная прямая проведена штрихами на рисунке 2. Именно к ней будет асимптотически стремиться (никогда не достигая) кривая зависимости удельной кинетической энергии от расстояния. Из рисунка видно, что теперь (с учетом силы сопротивления) эта кривая пересечет прямую \(~\frac{\upsilon^2_*}{2}\), соответствующую наименьшей требуемой скорости υ_*, при H’_* > H_*. Если вообще пересечет — для этого нужно соблюдение условия \(~\frac{\upsilon^2_m}{\upsilon^2_*} > 1\). Тогда, разделив друг на друга равенства (7) и (5), получим

\(~\frac{mNK}{M + m} > 1\) .

Видно, что друзей надо приглашать побольше (увеличивать N) или делать планер полегче (уменьшать М) и аэродинамически совершеннее (увеличивать К). Все это очевидно, но теперь можно ответить и на вопросы «сколько?».

И еще одно важное наблюдение сделаем, не решая уравнение (6), а лишь слегка преобразовав его. Используем характерную скорость υ_m в качестве масштаба скоростей. Для этого уравнение (6) разделим на равенство (7) и на суммарную массу M₀:

\(~\Delta \left(\frac{\upsilon}{\upsilon_m}\right)^2 = \left(1 - \left(\frac{\upsilon}{\upsilon_m}\right)^2 \right) \left( \frac{CS \rho}{K M_0}\right) \Delta y\) . (8)

Теперь видно, что и расстояние Δy просто напрашивается отнести к некоторой характерной величине, имеющей размерность длины. Она уже приготовлена во вторых скобках правой части уравнения. Обозначим ее через h:

\(~h = \frac{K M_0}{CS \rho}\) .

Пусть, например, качество планера соответствует К ~ 10, площадь его крыла S ~ 10 м², суммарная масса всей движущейся системы M₀ ~ 10³ кг, плотность морозного воздуха ρ ~ 1 кг/м³, а безразмерный коэффициент подъемной силы С ~ 1. Тогда h ~ 10 м.

Введенная нами h — не случайная комбинация букв. Она действительно характеризует то расстояние, на котором скорость «почти» достигает своего максимального значения, или, как говорят физики, релаксирует к установившемуся значению. Поэтому h можно назвать длиной релаксации.

Сказанного уже вполне достаточно. Но уж совсем Любопытный Читатель может потребовать точную зависимость скорости планера от расстояния. Пожалуйста. Для этого нужно просто решить уравнение (8), добавив к нему начальное условие: при y = 0 скорость планера υ = 0. Учтем еще, что \(~\Delta \left(\frac{\upsilon}{\upsilon_m}\right)^2 = -\Delta \left(1 - \left(\frac{\upsilon}{\upsilon_m}\right)^2 \right)\), поскольку знак приращения Δ «съедает» любую постоянную, в том числе и единицу, и введем новую переменную

\(~\beta = 1 - \left(\frac{\upsilon}{\upsilon_m}\right)^2\) .

Тогда уравнение (8) запишется в виде

\(~d \beta = -\beta \frac{dy}{h}\) .

Это уравнение широко известно в науке. Например, оно может описывать распад радиоактивных элементов (тогда y играет роль времени, a h — периода полураспада) или изменение популяции микробов в банке (тогда h отрицательно). В нашем случае решение последнего уравнения с упомянутым начальным условием имеет вид (не верите — спросите любого прохожего):

\(~\left(\frac{\upsilon}{\upsilon_m}\right)^2 = 1 - e^{-\frac yh}\) .

И теперь уж Догадливый Студент, измерив высоту общежития Н, точно может сказать, сколько Преданных Друзей нужно пригласить, чтобы его планер достиг необходимой скорости.

Но где взять планер? Подсчитав все затраты и предвидя еще возражения коменданта общежития, мэрии, муниципалитета, самих Преданных Друзей и, наконец, возможную оттепель (при которой нужно учесть еще и силу трения о крышу), он понял, что дешевле купить авиабилет. Так что — летайте самолетами...