Слободянюк А.И. Физика 10/4.7. Статика – законы равновесия тел
Материал из PhysBook.
§4. Основные законы динамики
4.7 Статика – законы равновесия тел.
Рассмотрим, при каких условиях тело может находиться в состоянии покоя, естественно, в какой либо инерциальной системе отсчета. На основании законов динамики И.Ньютона можно сформулировать два обязательных условия равновесия.
1. Векторная сумма внешних сил, действующих на тело, должна быть равна нулю. Нами было показано, что ускорение центра масс тела полностью определяется внешними силами, действующими на рассматриваемое тело. Если эта сумма равна нулю, то ускорение центра масс тела равна нулю. Поэтому можно выбрать такую систему отсчета, в которой центр масс покоится. Заметим, что при вычислении суммы векторов, нас не интересуют точки приложения различных сил, нам важны только величины и направления этих сил. Поэтому, говорят, что при рассмотрении поступательного движения все векторы сил можно переносить параллельно самому себе.
Так как центр масс твердого тела жестко связан с самим телом, то при покоящемся центре масс, тело может только вращаться вокруг оси, проходящей через центр масс. Для того, чтобы тело не начало вращаться необходимо, выполнение второго условия равновесия.
2. Сумма моментов внешних сил, действующих на тело, должна быть равна нулю. Согласно определению, момент силы зависит не только от величины и направления этой силы, но и от оси вращения. Поэтому, говоря о покоящемся теле, встает вопрос, относительно какой оси должны вычисляться моменты действующих сил. Ответ на данный вопрос следующий – для покоящегося тела суммарный момент равен нулю для любой мыслимой оси вращения! К счастью, при рассмотрении условий равновесия нет необходимости рассматривать все возможные оси вращения (что в принципе невозможно). Можно показать, что если векторная сумма сил равна нулю и сумма моментов сил относительно какой-либо оси равна нулю, то и сумма моментов сил относительно любой другой параллельной оси также равна нулю.
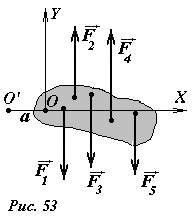
Проиллюстрируем это положение простым примером. Пусть силы, действующие на тело, лежат в одной плоскости и параллельны друг другу (рис. 53). Введем систему координат XOY, одна из осей которой X перпендикулярна направлению действия сил и проходит через ось вращения O. Обозначим координаты точек приложения сил x1, x2, x3… , тогда суммарный момент сил относительно этой оси равен
 .
.
Вычислим момент сил относительно оси O’, отстоящей от оси O на расстоянии a
 .
.
Как следует из полученного соотношения, при (F1 + F1 + F2 + F3 + … ) = 0 M’ = M. То есть, если сумма сил равна нулю, то суммарные моменты сил, относительно всех параллельных осей, равны.
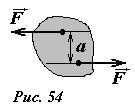
Практически важным является случай, когда не тело действуют две силы, равные по величине и противоположные по направлению, но приложенные к разным точкам (в этом случае говорят о паре сил). Момент пары сил не зависит от оси вращения и равен M = aF (где F - модуль каждой силы, a - расстояние между линиями действия сил).