Слободянюк А.И. Физика 10/4.4
§4. Основные законы динамики
4.4 Поступательное движение твердого тела.
Мысленно разобьем произвольное твердое тело на столь малые части, чтобы каждую из них можно было рассматривать как материальную точку, к которым применимы три закона динамики И.Ньютона.
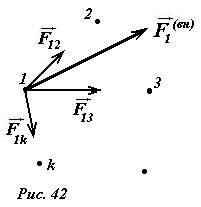
Рассмотрим произвольную систему материальных точек (рис. 42), которые взаимодействуют между собой (эти силы назовем внутренними) и с другими телами, не входящими в рассматриваемую систему (внешние силы).
Пронумеруем эти точки. В соответствии со вторым законом Ньютона для каждой материальной точки (например, номер 1) справедливо уравнение
где m1 - масса рассматриваемой точки; \(~\vec a_1\) - ее ускорение; \(~\vec F_{12}, \vec F_{13}, \ldots , \vec F_{1k}\) - силы [1], действующие на точку 1, со стороны материальных точек 2,3,…k…; \(~\vec F_1^{vn}\) - сумма внешних сил, действующих на точку 1. Просуммируем уравнения вида (1) для всех точек, включенных в рассматриваемую систему, в результате чего получим очень громоздкое уравнение
В этом уравнении силы взаимодействия между двумя материальными точками взаимно уничтожаются (!), в соответствии с 3 законом Ньютона. Например, \(~\vec F_{12} = -\vec F_{21}\) , поэтому \(~\vec F_{12} + \vec F_{21} = 0\) . Таким образом, в правой части уравнения (2) остается сумма только внешних сил, действующих на систему:
При поступательном движении твердого тела ускорения всех точек тела одинаковы \(~\vec a_1 = \vec a_2 = \vec a_3 = \ldots = \vec a\) , поэтому уравнение (3) еще больше упрощается и приобретает вид, совпадающий с уравнением 2 закона Ньютона для материальной точки,
в котором \(~\vec F\) - сумма внешних сил, действующих на тело, m - масса тела.
Итак, при поступательном движении твердого тела, ускорение тела пропорционально сумме внешних сил, действующих на тело и обратно пропорционально массе тела.
Обратите внимание, что обоснование применимости уравнения второго закона (4) к движению твердого тело потребовало также привлечения третьего закона Ньютона.
Примечания
- ↑ Обращайте внимание на индексные обозначения сил взаимодействия: здесь первый индекс указывает номер тела, на которое действует сила, со стороны тела, номер которого указывает второй индекс. Некоторые авторы предпочитают противоположную индексацию.