Слободянюк А.И. Физика 10/2.5

Содержание книги

Предыдующая страница

§2. Кинематическое описание механического движения материальной точки

2.5 Векторные характеристики движения материальной точки

Положение точки в пространстве можно задать с помощью вектора, соединяющего начало координат с данной точкой - такой вектор называется радиус-вектором точки, мы будем обозначать его символом \(~\vec r\). Очевидно, что координаты этого вектора, совпадают с координатами точки (x,y,z) , поэтому мы оставим эти обозначения и для координат радиус-вектора.

Если тело изменяет свое положение в пространстве, то его радиус-вектор будет изменяться с течением времени, то есть станет функцией времени. Зависимость радиус-вектора от времени \(~\vec r(t)\) будет являться законом движения.

Изменение положения в векторной форме удобно описывать с помощью вектора перемещения \(~\vec S\) - вектора, соединяющего начальное \(~\vec r_0\) и конечное положение \(~\vec r_1\) движущейся точки. Вектор перемещения равен разности радиус-векторов конечного и начального положения (см. рис.10)

\(~\vec S = \vec r_1 - \vec r_0\) . (1)

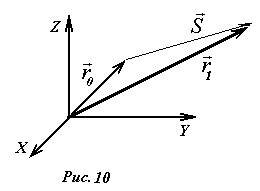
Отношение изменения радиус-вектора к промежутку времени, за который это изменение произошло, называется средним вектором скорости (или просто средней скоростью):

\(~\vec \upsilon_{cp}= \frac{\Delta \vec r}{\Delta t}\) . (2)

Если промежуток времени, за который измеряется изменения радиус-вектора, сделать очень малым (предельно малым), то вектор средней скорости перейдет в вектор мгновенной скорости

\(~\vec \upsilon = \frac{\Delta \vec r}{\Delta t}\) , при Δt → 0 . (3)

Это определение является наиболее общим определением скорости. Заметим, что при постоянном векторе скорости тела его траекторией обязательно является прямая линия.

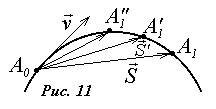
Выясним, как направлен вектор мгновенной скорости по отношению к произвольной траектории движения материальной точки. Пусть тело (которое мы считаем материальной точкой) переместилось за промежуток времени Δt по некоторой траектории из точки A₀ в точку A₁ (см. рис.11). Вектор средней скорости совпадает по направлению с вектором перемещения \(~\vec S\) . При уменьшении рассматриваемого промежутка времени Δt точка A₁ будет находиться все ближе к точке A₀, соответственно, будет изменяться и вектор перемещения, при Δt → 0 вектор перемещения будет стремиться к касательной к траектории, поэтому вектор мгновенной скорости направлен вдоль касательной к траектории.

Вектором ускорения \(~\vec a\) называется отношение изменения вектора скорости к промежутку времени, в течение которого это изменение произошло, при стремлении этого промежутка к нулю:

\(~\vec a = \frac{\Delta \vec \upsilon}{\Delta t}\) , при Δt → 0 . (4)

Подчеркнем, что в данном определении ускорения фигурирует изменение вектора скорости - а вектор может изменяться как по величине, так и по направлению. Следовательно, непрямолинейное (криволинейное) движение тела обязательно является движением с ускорением (так как изменяется направление вектора скорости).

Простейшие модели движения.

Реальные движения реальных тел, как правило, довольно сложны – разгон, торможения, повороты, скорости, ускорения тел постоянно изменяются. Однако во многих случаях для описания движения можно использовать достаточно простые (конечно, приближенные) модели, к рассмотрению которых мы сейчас и приступим.

Следующая страница