Слободянюк А.И. Физика 10/19.1.II
§19. Волновые процессы
19.1 Кинематическое описание волнового процесса.
19.1.2 Описание монохроматических волн на плоскости и в трехмерном пространстве.
Легкие волны, плавно набегающие на берег озера, ласковое волнение теплого моря, гигантские валы штормящего океана – наиболее очевидные примеры волн, распространяющихся по плоскости.
Как отметил известный английский физик лорд Рэлей волны на поверхности волны наиболее часто используемый пример волновых процессов, и наиболее неудачный из них. Причина такого высказывания заключается в том, что поверхностные волны чрезвычайно сложны для математического описания: так эти волны не являются ни поперечными, ни продольными; существует, по крайней мере, два механизма возникновения поверхностных волн (гравитационный и капиллярный); их профиль далек от синусоидального и изменяется по мере распространения, даже может становиться неустойчивым и опрокидываться; их скорость зависит от высоты волны. Строгой теории этих волн не существуют до настоящего времени. Тем не менее, мы постоянно будем использовать волны на поверхности воды для иллюстрации изучаемых волновых явлений. Наблюдение и экспериментальное изучение этих явлений настолько просто и знакомо, что искупает отмеченные «недостатки». Наконец, если эти волны не слишком велики, то поддаются описанию в рамках простейших гармонических волн. И последнее, неудачу того или иного эксперимента с поверхностными волнами всегда можно списать на их уникальность.
Для описания поверхностных волн удобно ввести на рассматриваемой плоскости систему координат, например, декартовую. Тогда любая физическая величина, изменяющаяся при переходе от одной точки плоскости к другой, может быть описана как функция двух переменных – координат точки на плоскости. Если же эта величина изменяется с течением времени, то для описания ее изменения необходимо использовать функцию трех переменных: двух пространственных координат и времени. Так и поверхностная волна должна описывается функцией этих трех переменных U(x,y,t). Физическая величина, определяемая этой функцией, может иметь разный смысл (в зависимости от того, волна какой природы описывается).
Так в случае произвольной волны на поверхности (Рис. 285) в качестве такой величины выступает высота уровня жидкости над равновесным горизонтальным уровнем невозмущенной поверхности водной глади. Построим декартовую систему координат, одна из осей которой Oz вертикальна, а две другие лежат в горизонтальной плоскости спокойной воды. В этом случае геометрическое описание формы волны может иметь вид z(x,y,t), где (x,y,z) - координаты точки на поверхности волны.
Так как, мы пытаемся описывать волны произвольной физической природы, то для возмущения мы оставим общее обозначение U(x,y,t). Трехмерный график этой функции (при фиксированном значении момента времени t = t0) можно наглядно представлять как соответствующий изгиб волнующейся поверхности.
При описании монохроматических волн зависимость от времени должна иметь вид, общий для гармонических функций времени
который путем традиционных тригонометрических преобразований, можно представить в эквивалентной форме
В этом виде функция A(x,y) - имеет смысл амплитуды колебаний в точке с координатами (x,y), а φ(x,y) - начальной фазы колебаний в этой же точке.
Аналогично можно задавать уравнение волны, распространяющейся в трехмерном пространстве. Правда в этом случае нет возможности наглядно графически изобразить эту волну, так как даже в заданный момент времени в каждой точке пространства определяется некоторая физическая величина, описывающая волновой процесс – поэтому ее «график» следует строить в четырехмерном пространстве, что сделать на двумерном листе бумаге затруднительно. Пространственные волны описываются функцией четырех переменных: времени и трех пространственных координат \(~U(x,y,z,t) = U(\vec r,t)\) - в каждый момент времени в каждой точке пространства определяется некоторая физическая величина. По-прежнему, смысл этой величины определяется физической природой волны – это может быть смещение частицы от собственного положения равновесия положения равновесия (в упругих волнах), избыточное давление (в звуковых волнах), напряженность электрического поля (в электромагнитной волне) и т.д. Обобщая полученное общее выражение для монохроматической волны (2) на случай волн в пространстве, функцию, описывающую такую волну, можно представить в виде
где функции A(x,y,z), φ(x,y,z) - также имеют смысл амплитуды и фазы волны в точке с координатами (x,y,z).
Отметим также, что физическая величина, описывающая волну, может быть векторной (например, напряженность электрического поля в электромагнитной волне). В этом случае функции U(x,y,z,t), A(x,y,z) являются векторами. Введение таких векторов обязательно для поперечных волн. Фазовая функция φ(x,y,z) всегда скалярная, так еще ни кто не додумался ввести вектор фазы колебаний.
Фазовая функция φ(x,y,z) в бегущей волне обязательно должна зависеть от координат. Если фаза колебаний постоянна во всех точках плоскости, то все точки среды колеблются в одной фазе, поэтому перемещения «гребней и впадин» не будет – такие колебания протяженных сред также возможны, они называются стоячими волнами, с ними мы познакомимся позднее. В этом же разделе мы будем «придумывать» функции, описывающие бегущие волны, в форме (2).
Введем еще одно очень полезное геометрическое понятие, помогающее наглядно представлять произвольные волны (в том числе и пространственные). При взгляде на волны, прежде всего, бросаются в глаза гребни этих волн. Зная функцию волны (2), можно математически определить места расположения гребней (в некоторый фиксированный момент времени t0) – в этих точках косинус принимает максимальное значение, которое, как обычно, равно единице. Это значение достигается, когда аргумент косинуса принимает значения
Геометрическое место точек удовлетворяющих этому условию и образует гребни волн, причем различным значениям n соответствуют разные гребни. Некоторым, может, больше нравятся впадины волн – они без труда могут записать условие, удовлетворяющее этим точкам. В общем случае можно выделить множество точек, колеблющихся в одной фазе, то есть удовлетворяющим условию
Геометрическое множество точек, колеблющихся в одной фазе, называется волновой поверхностью[1]. Еще раз подчеркнем, что каждая волновая поверхность задается в конкретный момент времени, эти поверхности движутся вместе с волнами. Задание (и изображение) множества волновых поверхностей позволяет достаточно наглядно представлять даже сложную волну – всегда можно считать, что эти поверхности совпадают с гребнями волн. Важнейшим свойством волновой поверхности заключается в том, что направление движения волны перпендикулярно волновой поверхности. В этом мы убедимся на рассматриваемых ниже примерах волн, при изучении которых мы будем постоянно использовать понятие волновой поверхности.
Изображение волны с помощью волновых поверхностей аналогично изображению электростатического поля с помощью построения эквипотенциальных поверхностей, далее мы построим и волновые аналоги силовых линий этого поля. В очередной раз мы убедимся, что различные физические явления описываются с помощью одних и тех же математических конструкций.
19.1.3 Плоская волна на плоскости и в трехмерном пространстве.
Простейшей поверхностной волной является волна, изображенная на рис. 286: последовательность параллельных равноотстоящих гребней. Такая волна получила название плоской. Разумно выбрать декартовую систему координат так, чтобы одна из осей (Oy) была направлена вдоль гребней волн, а вторая (Ox) перпендикулярно им. При таком выборе системы координат функция волны не зависит от координаты y. Это не означает, что волна бежит только по оси Ox, просто при изменении координаты y (параллельном переносе вдоль этой оси) все характеристики волны остаются неизменными. Поэтому достаточно рассмотреть эту волну в единственной плоскости, перпендикулярной оси Oy. В этой плоскости сечение волны ничем не отличается от волны, распространяющейся вдоль прямой, поэтому может быть описана функцией
причем смысл всех параметров этой функции (амплитуда, круговая частота, волновое число) остается прежним. Функция (3) задает волну, распространяющуюся в положительном направлении оси Ox, изменение знака перед волновым числом изменяет направление движения волны. Волновые поверхности этой волны представляют собой параллельные прямые, перпендикулярные оси Ox, то есть перпендикулярные направлению распространения волны.
Если требуется рассмотреть несколько плоских волн, движущихся в различных направлениях, то уравнения этих волн нельзя задать в форме (3), ведь нельзя же выбрать единственную ось координат Ox, так чтобы она была перпендикулярна всем гребням! Поэтому уравнение (3) необходимо обобщить на случай произвольного направления движения плоской волны.
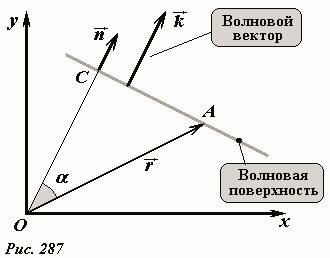
Рассмотрим плоскую волну, распространяющуюся в произвольном направлении (Рис. 287). Ее волновой фронт является прямой линией. Обозначим вектор единичной нормали к волновой поверхности \(~\vec n\). Этот вектор указывает направление распространения волны. Проведем также отрезок ОС, перпендикулярный волновой поверхности и проходящий через начало координат. Возьмем произвольную точку A, находящуюся на волновой поверхности, положение которой задается радиус-вектором \(~\vec r\). Найдем скалярное произведение этого радиус-вектора и вектора нормали
здесь α - угол между векторами сомножителями. Найденное произведение равно расстоянию от начала координат до волновой поверхности, следовательно, оно одинаково для всех точек, лежащих на волновой поверхности. Таким образом, уравнение волновой поверхности можно записать в компактной форме
где \(~\vec n\) - нормаль к плоскости, L - расстояние от плоскости до начала координат. При изменении постоянной L уравнение (6) будет описывать другую плоскость, параллельную данной, которая также будет являться волновой поверхностью для рассматриваемой волны. Поэтому множество волновых поверхностей может быть описано в форме \(~(\vec n \cdot \vec r) = \operatorname{const}\). Обратимся к общему уравнению волны (2) и заметим, что в качестве фазовой функции можно подставить функцию пропорциональную \(~(\vec n \cdot \vec r)\):
так точки, радиус-вектор которых удовлетворяет условию (6) будут находиться на одной фазовой плоскости. Наконец, вспомним, что скалярное произведение \(~(\vec n \cdot \vec r)\) равно расстоянию от волнового фронта до начала координат, то есть играет такую же роль, как переменная x в функции (5), описывающей волну, распространяющуюся вдоль оси Ox. Поэтому константа в выражении (7) является волновым числом \(~k = \frac{2 \pi}{\lambda}\). Следовательно, уравнение произвольной плоской волны имеет вид
Из этого уравнения видно, что имеет смысл ввести новый вектор, характеризующий волну
модуль которого равен волновому числу \(~|\vec k| = \frac{2 \pi}{\lambda}\), а направление совпадает с нормалью к волновой поверхности, то есть указывает направление распространения волны. Построенный таким образом вектор называется волновым вектором. Используя это понятие, уравнение плоской волны приобретает окончательный вид
Можно провести аналогию с построением вектора скорости: модуль этого вектора равен скорости движения, а направление указывает направление перемещения.
К уравнению плоской волны в форме (8) можно было прийти гораздо быстрее, осуществив поворот системы координат, направив «новую» ось Ox вдоль нормали к волновому фронту и заметив, что «новое» значение x равно произведению \(~(\vec n \cdot \vec r)\). Однако, мы использовали «окружной» путь, который является общим и будет использован нами при построении уравнений других волн.
Если кого-то не убедили до конца наши рассуждения, может записать уравнение (10) в явном координатном виде
(где β - угол между направлением распространения волны и осью Ox) и построить с помощью компьютера трехмерный профиль этой волны – при безошибочном построении вы увидите нужную волну.
Волны более сложные, чем плоские могут менять направление своего распространения (вспомните, хотя бы, отражение и преломление). В каждой точке области распространения волны определяется волновой вектор, который указывает направление распространения волны. Следовательно, в очередной раз мы встречаемся с такой математической конструкцией, как векторное поле – поле волновых векторов. Поэтому, как и для любого векторного поля, можно построить его «силовые линии». В данном случае, такие линии называется волновыми лучами. Волновой луч - направленная линия, касательная к которой совпадают с направлением волнового вектора в данной точке.
Семейство лучей, также иллюстрирует распространяющиеся волны, как и семейство волновых поверхностей. Таким образом, мы получаем полную аналогию с описанием электростатического поля: аналогом эквипотенциальной поверхности является волновая поверхность; аналогом силовых линий являются волновые лучи. В этом смысле плоская волна аналогична однородному полю, поэтому является наиболее простой волной.
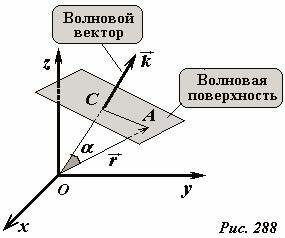
Полученные результаты, описывающие плоские волны, легко обобщаются на трехмерный случай. Волновые поверхности плоской волны являются параллельными плоскостями, перпендикулярными направлению распространения волны, а волновые лучи. Для вывода уравнения волны достаточно сделать рис. 287 трехмерным (рис. 288), повторить все рассуждения, приведшие нас к уравнению (10) и просто его еще один раз переписать
В этом уравнение скалярное произведение \(~(\vec k \cdot \vec r)\) есть произведение трехмерных векторов: волнового \(~\vec k\) и радиус-вектора \(~\vec r\). Множество точек, для которых это произведение постоянно, является плоскостью, перпендикулярной волновому вектору. Действительно, для всех точек, лежащих на плоскости, это скалярное произведение можно представить в виде
где |OC| - расстояние от плоскости до начала координат, поэтому оно постоянно.
Если выбрать ось Ox так, чтобы она совпадала с направлением распространения плоской волны, то уравнение последней имеет наиболее простой вид
В этом выражении явно отсутствуют координаты y и z, возмущение среды зависит только от одной координаты x, поэтому все точки, лежащие в плоскости, перпендикулярной оси Ox колеблются одинаково, то есть эти плоскости являются волновыми поверхностями.
19.1.4 Круговая волна на плоскости и сферическая волна в трехмерном пространстве.
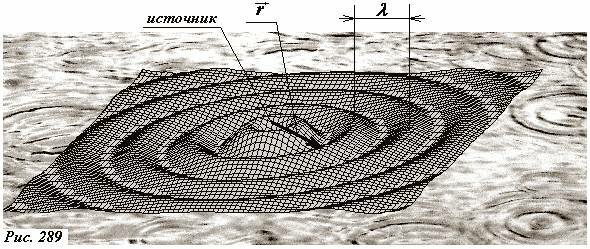
Законы симметрии действуют и в волновых процессах – симметрия волн повторяет симметрию их источников. Если источник поверхностной волны является точечным, то все направления от источника являются равноправными, поэтому волна должна иметь осевую симметрию, ее возвышения и впадины, ее волновые поверхности должны быть круговыми. Хорошим примером точечного источника является капля дождя, упавшая на поверхность лужи (Рис. 289).
Учитывая симметрию системы, заключаем, что характеристики волны должны зависеть только от расстояния r до источника. Этому условию удовлетворяет функция
описывающая установившуюся круговую волны. Обратите внимание, на отличие этой функции от функции, описывающей плоскую волну: в данном выражение пространственная часть фазы равна произведению волнового числа \(~k = \frac{2 \pi}{\lambda}\) (а не волнового вектора, как в случае плоской волны) на расстояние до центра волны, которое выражается через декартовые координаты точки наблюдения \(~r = \sqrt{x^2 + y^2}\) (если начало координат совпадает с источником). В случае круговой волны, волновой вектор не является постоянным, так как его направление, указывающее направления распространения волны, изменяется от точки к точке. Этот вектор направлен радиально от источника, поэтому может быть записан в виде
где \(~\vec r\) - вектор, проведенный от источника до точки наблюдения.
Эта запись аналогична выражению для направления вектора напряженности электрического поля, созданного точечным зарядом.
Если в трехмерном пространстве волна возбуждается точечным источником, то эта волна должна иметь сферическую симметрию, то есть ее волновые поверхности являются сферами, концентрическими с источником. Такая сферическая волна описывается функцией, вид которой совпадает с выражением (1), в котором \(~r = \sqrt{x^2 + y^2 + z^2}\) есть расстояние до источника в трехмерном случае (при этом считаем, что начало системы координат совпадает с источником волны).
Амплитуда круговой и сферической волн A(r) также должна зависеть от расстояния до источника. Если источник представляет собой некоторое небольшое тело, совершающее незатухающие гармонические колебания с частотой ω (которая определяет частоту волны), то даже в этом случае амплитуда волны должна убывать по мере удаления от источника. Вид этой зависимости можно установить на основании достаточно простых рассуждений[2]. По аналогии с гармоническим колебаниями, можно заключить, что, энергия, переносимая волной, пропорциональна квадрату амплитуды волны.
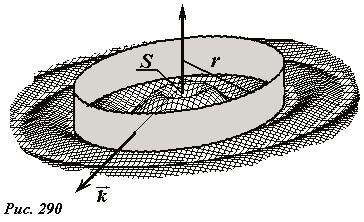
Действительно, и кинетическая энергия частиц движущейся среды, и изменение потенциальной энергии их при смещении от положения равновесия пропорциональны квадрату амплитуды. Окружим точечный источник поверхностной круговой волны цилиндрической поверхностью, ось которой проходит через источник S (Рис. 290). Если пренебречь затуханием волны, то энергия, переносимая в единицу времени через такую цилиндрическую поверхность, равна мощности источника волны, и не зависит от ее радиуса r.
Так как плотность потока энергии пропорциональна квадрату амплитуды и постоянна на поверхности цилиндра, а его пропорциональна радиусу, то справедливо соотношение
из которого следует зависимость амплитуды незатухающей круговой волны от расстояния до источника
где постоянная величина A0 зависит от мощности источника.
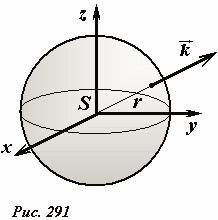
Аналогичные рассуждения применимы и для сферической трехмерной волны. Здесь поток энергии через любую сферу концентрическую с источником не зависит от радиуса сферы (Рис. 291). Этот поток пропорционален квадрату амплитуды волны, которая постоянна на поверхности сферы, а ее площадь пропорциональна квадрату радиуса, то при отсутствии потерь энергии справедливо выражение (аналогичное (3))
Поэтому амплитуда сферической волны обратно пропорциональна расстоянию до источника
Таким образом, окончательно получаем, что поверхностная круговая и пространственная сферические волны описываются уравнениями
соответственно.
В полученных выражениях формально при r → 0 амплитуда волны стремиться к бесконечности. Но не будем забывать, что точечный источник волны является абстрактной моделью, любой реальный источник имеет конечный размеры. Кроме того, волновое поле вблизи источника описывается более сложными формулами. Поэтому полученные выражения (7)-(8) справедливы на больших расстояниях от источника (по крайней мере, больше длины волны).
Рассмотренные нами волны являются простейшими моделями реальных волн в изобилии окружающих нас в реальном мире. Конечно, реальные волны имеют более сложную структуру, но многие из них могут быть представлены в виде суперпозиции простейших плоских и сферических волн. Но чтобы пользоваться принципов суперпозиции его необходимо обосновать, что можно сделать только на основании физических законов, не говоря уже о том, что необходимо показать, «придуманные нами» кинематические модели действительно описывают реальные волны. Поэтому мы сейчас вынуждены обратиться к физическим законам, описывающим движение реальных систем.