Слободянюк А.И. Физика 10/17.4

Содержание книги

Предыдующая страница

§17. Механические колебания

17.4 Качественный анализ движения материальной точки.

Во многих случаях характер поведения механической системы может быть проанализирован без точного решения уравнений движения. В данном разделе мы рассмотрим один из методов такого качественного анализа.

Пусть материальная точка массы m может двигать вдоль прямой, с которой мы совместим ось Ox декартовой системы координат. Для расчета закона движения этой точки используется уравнение второго закона Ньютона

\(~ma = F\) , (1)

где a - ускорение точки, F - сумма всех сил, действующих на материальную точку (точнее сумма проекций сил на выбранную ось). В общем случае силы, действующие на тело, могут быть постоянными, а также зависеть от времени, координаты точки, от ее скорости. Поэтому с математической точки зрения уравнение (1) следует рассматривать как уравнение относительно неизвестной функции x(t) - закона движения. Помимо самой неизвестной функции в это уравнение входят ее производные: первая производная x′ = υ(t) - мгновенная скорость точки, вторая производная x′′ = a - ее ускорение. При задании начальных условий (начальной координаты и начальной скорости) это уравнение имеет единственное решение, которое и определяет точный закон движения материальной точки. Однако, в большинстве случаев точное решение уравнения (1) вызывает значительные математические трудности, поэтому очень часто его решают численно с помощью компьютера. Один из простейших методов такого численного решения был рассмотрен нами при изучении кинематики.

Если сумма всех сил, действующих на тело, равна нулю, движение такого тела является равномерным. Если все силы, действующие на тело, постоянны (как по величине, так и по направлению), то и их сумма также постоянна. В этом случае движение тела является равноускоренным и его описание не вызывает никаких сложностей.

17.4.1 Автономные системы.

Многие из уже изученных нами сил зависят от положения тела (его координаты). Такими силами являются силы всемирного тяготения, силы электростатического взаимодействия, силы упругости. Если на тело действую только такие силы, то уравнение движения (1) приобретает вид

\(~ma = F(x)\) . (2)

Такая физическая система, уравнения движения корой не содержат в явном виде ни времени, ни скорости частиц, называется автономной. Поведение таких систем можно качественно проанализировать на основании закона сохранения механической энергии. Преобразуем уравнение (1) следующим образом. Запишем выражение для ускорения как «скорость изменения скорости» \(~a = \frac{\Delta \upsilon}{\Delta t}\) и умножим уравнение на Δx - малое изменение координаты тела

\(~m\frac{\Delta \upsilon}{\Delta t} \Delta x = F(x) \Delta x\) . (3)

В этом уравнении величина \(~m\frac{\Delta \upsilon}{\Delta t} \Delta x = m \Delta \upsilon \frac{\Delta x}{\Delta t} = m \upsilon \Delta \upsilon = \Delta \left( \frac{m \upsilon^2}{2} \right)\) есть изменение кинетической энергии тела на малом интервале изменения его координаты. Величина \(F(x) \Delta x = \delta A\) является работой, совершенной над телом на этом же интервале изменения координаты. Так как силы, действующие на рассматриваемое тело, зависят только от координаты, то работа этих сил может быть представлена как уменьшение потенциальной энергии тела \(\delta A = −\Delta U\) . Понятно, что потенциальная энергия является некоторой функцией от координаты тела U(x). Таким образом, проведенные математические преобразования приводят нас к уравнению закона сохранения механической энергии: увеличение кинетической энергии тела равно убыли его потенциальной энергии; или сумма кинетической и потенциальных энергий тела остается постоянной

\(~\frac{m \upsilon^2}{2} + U(x) = \operatorname{const}\) . (4)

Константа в этом уравнении имеет смысл полной механической энергии движущегося тела E и может быть определена из начальных условий.

Связь между потенциальной энергией и действующей силой следует из сравнения выражений для работы произведенной над телом \(F(x) \Delta x = - \Delta U\) , откуда находим, что сила равна производной от потенциальной энергии по координате, взятой с противоположным знаком

\(~F(x) = -\frac{\Delta U}{\Delta x} = -U'(x)\) . (5)

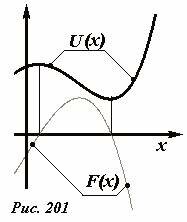
Связь между этими двумя функция может быть проиллюстрирована и графически (Рис. 201): если функция U(x) возрастает, то F(x) отрицательна; если U(x) убывает, то F(x) положительна; в точках экстремумов функции U(x) функция F(x) обращается в нуль. Следует также запомнить, что действующая сила всегда направлена в сторону убывания потенциальной энергии. Отметим также, что выражение (5) определяет потенциальную энергию с точностью до постоянного слагаемого – с этим, парадоксальным на первый взгляд, обстоятельством мы уже неоднократно встречались.

Подобный вывод мы уже проводили, при рассмотрении закона сохранения энергии. Здесь же подчеркнем, что сделанные нами преобразования носят математический характер, поэтому, если удалось получить уравнение движения вида (2), то всегда можно перейти к эквивалентному уравнению (4), в котором функция U(x) удовлетворяет соотношению (5) – не зависимо от того, является ли функция F(x) силой, а U(x) - потенциальной энергией. Напомним, для того, чтобы ввести понятие потенциальной энергии для того или иного вида взаимодействия, необходимо доказать, что это взаимодействие является потенциальным, то есть что работа не зависит от вида траектории, а определяется только начальным и конечным положением. Такие силы называются консервативными, и системы, в которых действую только такие силы, также называются консервативными. В некоторых случаях удается провести преобразование от уравнения (2) к уравнению (4) даже если нельзя говорить строго о потенциальной энергии, в такой ситуации функцию U(x) называют эффективной потенциальной энергией.

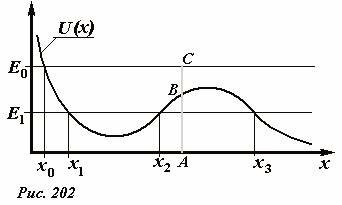
Дадим теперь наглядную геометрическую иллюстрацию уравнения (4). Для этого построим график зависимости потенциальной энергии тела от его координаты U(x) (На Рис. 201 приведен пример возможной зависимости). График зависимости потенциальной энергии от координаты называют потенциальной кривой. На этом же графике проведем горизонтальную прямую, соответствующую уровню полной механической энергии точки. Пусть, например, эта энергия равна E₀ . В точке с произвольной координатой A длина вертикального отрезка AB равна потенциальной энергии тела, длина отрезка AC - есть полная энергия тела, следовательно, длина отрезка BC выражает кинетическую энергию рассматриваемого тела. Так как кинетическая энергия не может быть отрицательной, то тело не может находиться в тех точках оси, где потенциальная энергия больше его полной энергии. Таким образом, горизонтальная прямая, проведенная на уровне полной энергии отсекает на потенциальной кривой допустимые области движения тела: только те, где потенциальная кривая лежит ниже прямой полной энергии. Так для уровня энергии E₀ (на Рис. 202) запрещенной является область x < x₀ , то есть движение точки возможно только при x₀ ≥ x. В точках пересечения уровня полной энергии с потенциальной кривой полная энергия равна потенциальной, следовательно, кинетическая энергия и скорость тела в этой точке обращается в нуль. Такие точки называются точками возврата.

Если полная энергия тела, в рассматриваемом примере уменьшится до значения E₁, то для него возникнет еще одна запрещенная область движения x₂ < x < x₃. В этом случае движение тела возможно либо в ограниченной области x₁ ≤ x ≤ x₂ (понятно, что в этом случае тело будет совершать колебания между указанными точками), либо в неограниченной с одной стороны области x ≥ x₃.

Таким образом, потенциальная кривая и уровень полной энергии определяют области движения тела.

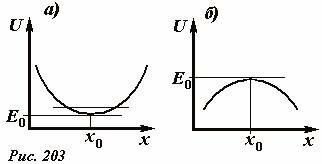
Весьма интересным случаем является совпадение уровня полной энергии E₀ с минимумом потенциальной энергии (Рис. 203 а).

Область, в которой потенциальная кривая содержит точку минимума, часто называют потенциальной ямой. В этой ситуации разрешенная область движения сужается до единственной точки x₀, которая является точкой равновесия: в этой точке сумма сил, действующих на тело равна нулю. Если же незначительно увеличить энергию тела, то оно начнет колебаться вокруг этой точки: при незначительном отклонении от положения равновесия возникают силы направленные к положению равновесия, стремящиеся вернуть тело в это положение. Такое положение равновесия называется устойчивым. Минимум потенциальной кривой указывает на точку устойчивого равновесия тела. Если полная энергия тела совпадает с максимумом потенциальной энергии (Рис. 203 б), в точке максимума тело также находится в состоянии равновесия, так как здесь сумма сил также равна нулю. Однако, при малом отклонении от этого положения скорость тела начинает возрастать – тело все дальше удаляется от положения равновесия. Такое положения равновесия является неустойчивым: при малом отклонении от него возникаю силы, стремящиеся еще дальше увести тело от этого положения. Так как в реальности, каждое тело подвержено незначительным внешним воздействиям, то тело в положении неустойчивого равновесия находиться длительное время не может.

Проведенные рассуждения становятся очевидными, если воспользоваться следующей аналогией (Рис. 204). В поле тяжести потенциальная энергия тела пропорциональна высоте \(U = mgh\), поэтому профиль потенциальной кривой совпадает с профилем поверхности, на которой находится рассматриваемое тело. Поэтому поведение тела в некотором потенциальном поле, описываем функцией U(x) полностью аналогично поведению шарика (чтобы трение было пренебрежимо малым), катающемуся по горке с профилем, совпадающим с потенциальной кривой.

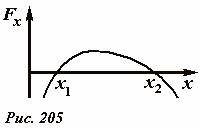
Анализ устойчивости положения тела можно провести и на основе рассмотрения зависимости результирующей силы от координаты. Для примера на Рис. 205 построен график зависимости проекции результирующей силы F_x, действующей на тело, от его координаты. Положениям равновесия соответствуют точки, в которых F_x = 0, на рисунке показаны две таких точки x₁, x₂. Что бы определить устойчивость необходимо мысленно сдвинуть тело на малое расстояние от положения равновесия. Так при смещении тела на небольшое расстояние δx в положительном направлении от точки x₁ результирующая сила положительна, следовательно, тело продолжит движение в том же направлении. Аналогично, при смещении в отрицательном направлении возникнет отрицательная сила, которая еще дальше будет уводить тело от точки x₁: следовательно, эта точка есть точка неустойчивого равновесия. Противоположна ситуация вблизи точки x₂: при малом смещении тела от этой точки возникает сила противоположного знака, которая возвращает тело к точке x₂, следовательно, это точка устойчивого равновесия.

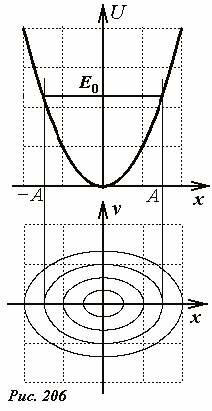
Наконец, еще одно общее рассуждение, касательно возможностей качественного анализа. Оказывается, потенциальные кривые прекрасно сочетаются с фазовыми траекториями - по заданной потенциальной кривой можно построить набор фазовых траекторий, соответствующих различным значениям полной энергии. Такой набор фазовых траекторий также называется фазовым портретом системы. Под графиком потенциальной кривой изобразим участок фазовой плоскости, так чтобы оси X были параллельны и начала их отсчета совпадали (рис.206).

Для примера рассмотрим потенциальную кривую, соответствующую гармоническим колебаниям. На графике потенциальной энергии зададим уровень полной энергии системы E₀ горизонтальной прямой, точки пересечения которой с потенциальной кривой определяют крайние точки - проводя вертикальные прямые их можно отметить на фазовой плоскости. Величину скорости при произвольном значении координаты можно оценить из разности полной и потенциальной энергии. Если же пользоваться компьютером, то можно построить точно. Из уравнения (4) выразим зависимость скорости от координаты

\(~\upsilon = \pm \sqrt{\frac{2}{m}(E_0 - U(x))}\) .

Как следует из этого выражения фазовая траектория симметрична относительно оси x , что понятно с точки зрения здравого смысла: в процессе колебательного движения за один период тело проходит каждую точку дважды - один раз в одном направлении, другой в противоположном, причем модули скорости при прохождении одной точки одинаковы. Как и следовало ожидать, движение точки является колебательным (можно даже уточнить – колебания гармонические), так как фазовые траектории являются эллипсами.

17.4.2 Диссипативные системы.

Если на тело, движущиеся вдоль оси Ox, действуют силы, приводящие к уменьшению механической энергии системы, то такие силы (и такие системы) называются диссипативными. Такие силы зависят от скорости, например, силы сопротивления воздуха, силы вязкого трения. Заметим, что даже сила сухого трения, подчиняющаяся закону Кулона-Амонтона, так же зависит от вектора скорости, так как эта сила всегда направлена в сторону противоположную вектору скорости.

С другой стороны, сила Лоренца, действующая на движущуюся заряженную частицу со стороны магнитного поля, также зависит от скорости, но не является диссипативной. Так как эта сила перпендикулярна вектору скорости, то она не совершает работы, следовательно, не изменяет энергии тела.

Качественно поведение таких систем также возможно проанализировать на основании рассмотрения потенциальной кривой. При наличии слабого затухания полная механическая энергия системы будет медленно уменьшаться, что соответствует медленному понижению уровня полной энергии.

Особенно наглядно можно провести такой анализ с помощью фазового портрета системы, построенного без учета потерь энергии.

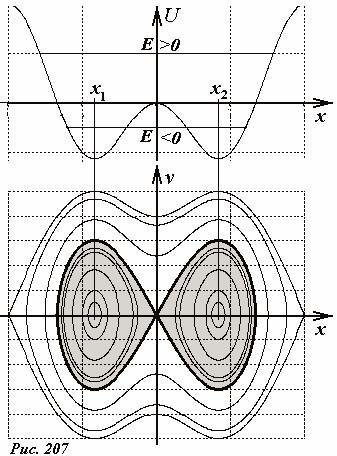
Пусть потенциальная кривая для некоторого тела имеет вид, показанный на рис. 207. Ниже построен фазовый портрет системы. Потенциальная кривая симметрична и содержит две точки минимума x₁, x₂ (две потенциальные ямы), соответствующие положениям устойчивого равновесия, разделенных точкой неустойчивого равновесия x = 0. В зависимости от величины полной энергии будет меняться и характер движения тела. Так при положительной энергии E > 0 тело движется симметрично относительно начала отсчета, огибая обе ямы. Когда тело проходит начало координат отсчета его скорость минимальна. Фазовые траектории в этом случае также симметричны и охватывают обе точки устойчивого равновесия x₁, x₂.

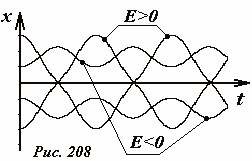
Если полная энергия тела отрицательна, то оно может двигаться только в одной из потенциальных ям – ему не хватает энергии, чтобы преодолеть потенциальный барьер, их разделяющий. В этом случае фазовые траектории также замкнуты, но охватывают только одну из точек устойчивого равновесия, какую именно - определяет начальное положение. Эта область на фазовом портрете на рисунке заштрихована. Графики зависимости координаты от времени для разных значений энергии и начальных положений точки показаны на рис. 208.

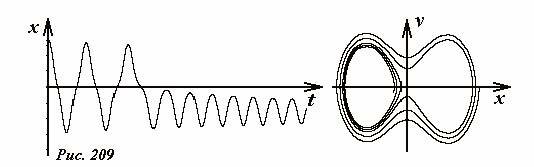
При наличии потерь малых потерь механической энергии фазовая траектория движения тела будет «сжиматься» переходя с одной фазовой траектории Рис. 207 на другую, соответствующую меньшей энергии. На рис. 209 показана одна из возможных фазовых траекторий, которая, в конце концов, придет к одному из положений устойчивого равновесия. Заметим, что предугадать в какую именно из двух потенциальных ям попадет тело практически невозможно: это зависит от начального положения тела, параметров сил трения, и даже если эти характеристики известны, может быть случайным.

17.4.3 Малые колебания в произвольных колебательных системах.

Проведенный анализ общих свойств колебательных систем показывает, что необходимым условием возможности колебательного движения в произвольной системе является наличие положения устойчивого равновесия. В этом случае при отклонении тела от положения равновесия возникнет возвращающая сила, направленная к положению равновесия. Под действием этой силы тело приобретет некоторую скорость, которая будет максимальна при достижении положения равновесия. Далее тело по инерции проскочит положение равновесия и отклонится от него в противоположную сторону. После чего процесс повторится. Таким образом, вторым условием возможности колебаний является наличие у системы инерционных свойств – тело нулевой массы свободно колебаться не может. При отсутствии сил трения процесс колебаний будет продолжаться бесконечно, если же силы трения значительны, то даже при наличии положения устойчивого равновесия колебания не возможны.

Рассмотрим теперь описание движения материальной точки вблизи положения устойчивого равновесия. Как и прежде будем основываться на уравнении второго закона Ньютона

\(~ma = F_x(x)\) , (1)

где F_x(x) - проекция результирующей силы на ось, вдоль которой движется тело.

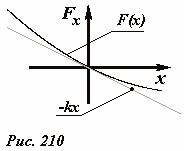
Совместим начало отсчета x = 0 с положением равновесия тела. В этой точке результирующая сила равна нулю F_x(0) = 0. Графически это выражается тем, что график зависимости F_x(x) пересекает ось Ox (Рис. 210) под некоторым отрицательным углом. При малом отклонении от положения равновесия функцию F_x(x) можно приближенно заменить линейной

\(~F_x(x) \approx - kx\) . (2)

График этой приближенной функции является прямой линией. Очевидно, что наименьшая погрешность приближения будет достигнута в том случае, если построенная прямая будет являться касательной к графику функции F_x(x). Следовательно, коэффициент наклона построенной прямой должен совпадать с производной функции F_x(x) в точке равновесия x = 0

\(~k = - F'_x(0)\) . (3)

Таким образом, если произвольную силу вблизи положения равновесия заменить линейным приближением (2) с коэффициентом пропорциональности (3), то уравнение движения преобразуется в уравнение гармонических колебаний

\(~ma = - kx\) , (4)

с частотой

\(~\omega = \sqrt{\frac{k}{m}} = \sqrt{-\frac{F'_x(0)}{m}}\) . (5)

Аналогичный результат модно получить и с помощью энергетического подхода к описанию движения рассматриваемого тела. Так закон сохранения механической энергии выражается уравнением

\(~\frac{m \upsilon^2}{2} + U(x) = E\) , (6)

где E - сохраняющаяся полная механическая энергия тела, U(x) - его потенциальная энергия. Положению устойчивого равновесия соответствует точка минимума функции U(x).

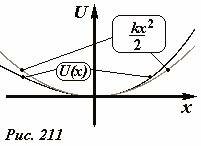
При малом отклонении от положения равновесия график этой функции можно приближенно описать параболой (Рис. 211)

\(~U(x) \approx \frac{k x^2}{2}\) . (7)

В этом выражении коэффициент пропорциональности k совпадает с коэффициентом в формуле (2). Для доказательства этого утверждения достаточно вспомнить формулу, связывающую потенциальную энергию с действующей силой: сила равно производной от потенциальной энергии, взятой с противоположным знаком \(F_x = - U'(x)\). Именно при записи приближенного выражения для потенциальной энергии в виде (7) из него непосредственно следует выражение (2):

\(~F(x) = -\left( \frac{k x^2}{2} \right)' = - kx\) .

Приближенная формула (7) для потенциальной энергии приводит к уравнению гармонических колебаний в форме

\(~\frac{m \upsilon^2}{2} + \frac{k x^2}{2} = E\) . (8)

Подведем итог общего рассмотрения: вблизи положения устойчивого равновесия тело может совершать колебания, если возвращающая сила может быть представлена в виде \(F_x(x) \approx -kx\), а потенциальная энергия в форме \(U(x) \approx \frac{k x^2}{2}\), то малые колебания являются гармоническими.

17.4.4 Математический маятник: не гармонические колебания.

Наиболее типичным и наглядным примером использования приближения малых колебаний является описание колебаний математического маятника. При больших углах отклонения использование приближения малых углов неприменимо, в этом случае необходимо искать решение точного уравнения движения

\(~\varepsilon = -\frac{g}{l} \sin \varphi\) , (1)

где ε - угловое ускорение маятника. К сожалению, это уравнение с математической точки зрения, очень сложно. Функции, являющиеся решениями этого уравнения при различных начальных условиях, не выражается через элементарные функции. Можно, конечно, решить это уравнение численно с помощью компьютера. Мы не будем рассматривать эти методы, ограничимся указанием принципиальных отличий решений уравнений (1) от приближения малых углов. Важнейшим из них является не гармоничность колебаний. Конечно, решениями этого уравнения являются периодические функции, которые по теории Фурье можно представить в виде суммы (бесконечной) гармонических функций кратных частот. Иными словами, в колебаниях математического маятника появляются кратные частоты – обертона.

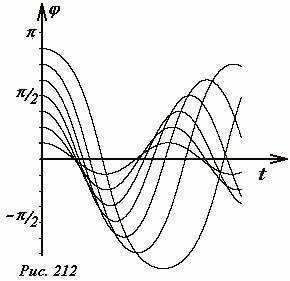
На Рис. 212 показаны графики зависимости угла отклонения маятника от времени при различных амплитудах колебаний, полученных с помощью численных расчетов. Конечно, определить на глаз являются ли полученными синусоидами, или нет невозможно.

Вторым важным отличием точного решения (1) от приближенного является зависимость периода колебаний от их амплитуды, что хорошо видно на Рис. 212. Покажем, как может быть рассчитана (опять же численно) эта зависимость. Пусть нить маятника отклонена на угол φ₀. Разобьем диапазон изменения координаты [-φ₀,φ₀] точки на малые интервалы \(~\Delta \varphi = \frac{\varphi_0}{N}\), тем самым получим набор точек разбиения \(\varphi_k = k \Delta \varphi\) , k = −N,−N + 1,... −1,0,+1,+2,...,+N.

Используя закон сохранения энергии для маятника

\(~\frac{m l^2 \omega^2}{2} - mgl \cos \varphi = - mgl \cos \varphi_0\) ,

мы можем вычислить скорости маятника ω_k в момент прохождения точек φ_k

\(~\omega_k = \sqrt{2 \frac{g}{l} (\cos \varphi_k - \cos \varphi_0)}\) .

На каждом интервале \(\Delta \varphi_k = \varphi_k - \varphi_{k-1}\) оценим среднюю скорость как среднее арифметическое значение скоростей на концах интервала \(\overline {\omega_k} = \frac{\omega_k + \omega_{k-1}}{2}\). Тогда время Δt_k, за которое маятник пройдет интервал \(\Delta \varphi_k = \varphi_k - \varphi_{k-1}\) можно найти по формуле \(~\Delta t_k = \frac{\Delta \varphi_k}{\overline {\omega_k}} = \frac{2 \Delta \varphi}{\omega_k + \omega_{k-1}}\), после чего останется только просуммировать эти значения по всем интервалам разбиения - полученная сумма будет равна половине периода колебания. Такой метод также является приближенным, но уменьшение шага разбиения всегда будет приводить к увеличению точности расчетов. Замена средней скорости среднеарифметическим является точной при равноускоренном движении, поэтому это приближение соответствует приближению равноускоренного движения на малом интервале.

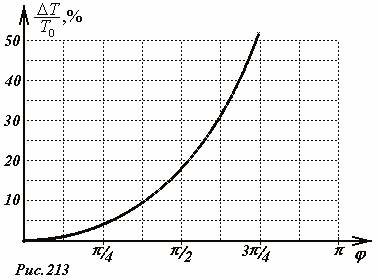
Не вдаваясь в технические детали расчета (при наличии времени и терпения его можно провести и на бумаге) приведем результаты расчета, полученные при разбиении диапазона изменения угла на двести равных интервалов. Результаты расчетов представлены на рис.213. Здесь, \(~T_0 = 2\pi \sqrt{\frac{l}{g}}\) - период малых колебаний, \(~\frac{\Delta T}{T_0} = \frac{T - T_0}{T_0}\)- относительное изменение периода колебаний при увеличении их амплитуды.

Имея эту кривую, можно ответить на вопрос, какие же колебания можно считать «малыми»? Ответ зависит от той точности, которая для вас является достаточной. Так, при амплитуде колебаний \(~\varphi_0 = \frac{\pi}{4}\) их период превышает период малых колебаний менее чем на 5%, а при амплитуде \(~\varphi_0 = \frac{\pi}{2}\) период возрастает всего на 18%. Отметим, что полученная зависимость приближенно может быть описана формулой

\(~T \approx T_0 \left(1 + \frac{\varphi^2_0}{16} \right)\) .

В заключение данного раздела укажем, что полученные результаты полностью подтверждаются экспериментальными данными.

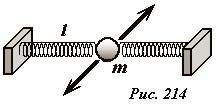
Рассмотрим еще один пример колебательной системы: небольшой шарик массы m расположен на гладкой горизонтальной поверхности и прикреплен с помощью двух пружин жесткости k длиной l к двум неподвижным упорам (Рис. 214). В положении равновесия все элементы системы находятся на одной прямой, при этом пружины не деформированы. Брусок совершает колебания в направлении перпендикулярном пружинам.

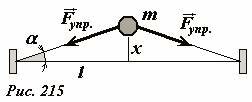
Положение шарика будем задавать его смещением x от положения равновесия. В процессе движения на шарик действуют силы упругости со стороны пружин (Рис. 215). Уравнение движения шарика имеет вид

\(~ma = -2 F_{ynp} \sin \alpha\) . (1)

Выразим силы упругости и синус угла отклонения через величину отклонения x, считая его малым. Для вычисления силы упругости воспользуемся законом Гука и приближенной формулой

\(~F_{ynp} = k \Delta l = k (\sqrt{l^2 + x^2} - l) = kl \left(\sqrt{1 + \frac{x^2}{l^2}} - l \right) \approx kl \left( \left( 1 + \frac{1}{2} \frac{x^2}{l^2}\right) - l \right) = \frac{k x^2}{2 l}\) .

Если считать отклонение малым, то и угол α также будет малым, поэтому

\(~\sin \alpha \approx \operatorname{tg} \alpha = \frac{x}{l}\) .

В этом приближении уравнение движения шарика будет иметь вид

\(~ma = -\frac{k}{2 l^2} x^3\) . (2)

Таким образом, даже малые колебания шарика в рассматриваемой системе не являются гармоническими. Аналитического решения полученного уравнения (2) также не существует. Анализ этого уравнения показывает, что период колебаний шарика в этой системе сильно зависит от амплитуды (даже при малых амплитудах): он убывает обратно пропорционально амплитуде.

То, что период гармонических колебаний не зависит от амплитуды, является в некотором смысле «счастливым совпадением»: при возрастании амплитуды, с одной стороны», колебаний возрастает путь, проходимый телом, с другой – возрастает средняя скорость движения. Для гармонических колебаний эти два фактора полностью компенсируют друг друга! Для математического маятника – путь возрастает быстрее, чем средняя скорость, поэтому период его колебаний незначительно возрастает при возрастании амплитуды. В рассмотренном примере средняя скорость возрастает значительно быстрее, чем путь, проходимый шариком – в этом случае период колебаний быстро убывает при возрастании амплитуды.

Примечания

Следующая страница