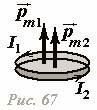Слободянюк А.И. Физика 10/13.1
§13. Взаимодействие магнитного поля с веществом
13.1 Намагниченность вещества.
Ранее мы ввели магнитную характеристику контура с электрическим током – его магнитный момент: вектор, модуль которого равен произведению силы тока на площадь контура \(p_m = IS\), и направленный по нормали к контуру. Укажем еще одно свойство этой характеристики – ее аддитивность: если система состоит из нескольких контуров, то магнитный момент такой системы равен векторной сумме магнитных моментов отдельных контуров.
Это свойство очевидно, если наложить два геометрически одинаковых контура друг на друга. В этом случае сложение моментов обосновывается сложением сил токов, текущих в контурах (Рис. 67).
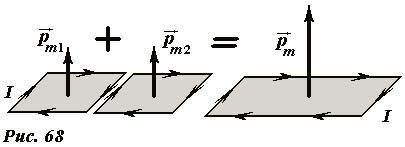
Легко также проиллюстрировать свойство аддитивности для двух плоских прямоугольных контуров с одинаковыми силами токов, если эти контуры приставить друг к другу, так, чтобы одна пара их сторон совпадала (Рис. 68).
В этом случае площадь образованного контура будет равна сумме площадей исходных, а результирующая сила тока в совпадающих сторонах будет равна нулю, так как эти токи текут в противоположных направлениях.
В конце концов, любая физическая характеристика придумана человеком для описания тех или иных свойств. Поэтому математические свойства этих характеристик обосновываются свойствами физических явлений, для описания которых придуманы эти характеристики. В магнитостатике малый контур с током играет двоякую роль: во-первых, он служит для обнаружения магнитного поля; во-вторых он является источником поля.
Правило сложения магнитных моментов может быть обосновано правилом сложения механических моментов[1]. Действительно, механический момент, действующий на контур в магнитном поле, пропорционален магнитному моменту контура. Поэтому для вычисления суммарного механического момента, действующего на систему, состоящую из нескольких контуров, можно сначала сложить магнитные моменты этих контуров.
Далее, контур с током создает магнитное поле, которое пропорционально магнитному моменту контура. Если поле создается системой из нескольких контуров, то для расчета суммарного поля по принципу суперпозиции необходимо просуммировать индукции полей, создаваемых каждым контуром, а можно сначала просуммировать магнитные моменты, а затем найти поле, создаваемое этим результирующим магнитным моментом.
Наконец, электрические дипольные моменты мы тоже складывали.
Если в магнитном поле каждая молекула вещества приобретает магнитный момент, то и все каждая часть объема вещества в целом приобретает некоторый магнитный момент, равный сумме магнитных моментов молекул, находящихся в этой выделенной части.
Таким образом, можно ввести характеристику воздействия магнитного поля на вещество – намагниченность. Намагниченностью (вектором намагниченности) вещества называется отношение суммарного магнитного момента выделенного части вещества к объему этой части
где \(~\vec p_{mk}\) - магнитный момент k -той молекулы, находящейся внутри выделенной части объема ΔV, суммирование проводится по всем молекулам, внутри этого объема.
Как обычно, чтобы сделать намагниченность точечной характеристикой, мы должны выделенную часть сделать бесконечно малой, или математически устремить ее объем к нулю ΔV → 0 . С физической точки зрения такой переход, строго говоря, невозможен, так как бессмысленно говорить о магнитном моменте выделенной части, если ее объем меньше объема молекулы. Поэтому, говоря об определении (1), мы подразумеваем достаточно малый объем, но в котором содержится достаточно много молекул.
Фактически данное определение намагниченности подразумевает пространственное усреднение характеристик магнитного поля, созданного отдельными электронами, атомами, молекулами. Если мысленно заглянуть внутрь вещества, то рассматриваемое магнитное поле резко изменяется в зависимости от расстояния до той или иной молекулы, кроме того, оно также является переменным во времени. Мы же рассматриваем некоторое поле, усредненное по объему, значительно превышающему объем отдельной молекулы, и по промежуткам времени, значительно превышающим периоды обращения электронов в атомах.
Примечания
- ↑ Очередной раз мы сталкиваемся с «терминологической бедностью» - одно слово «момент» описывает различные характеристики.