Перемещение. Траектория. Путь.
Материал из PhysBook
Рассмотрим движение материальной точки из начальной позиции 1 в конечную позицию 2 (рис.1.1). Начальное положение точки в момент времени t1 oтносительно точки отсчета О и связанной с ней системой координат ( X Y Z) однозначно определяется радиусом-вектором  , а конечное - в момент времени t2 - радиусом-вектором
, а конечное - в момент времени t2 - радиусом-вектором  .
.
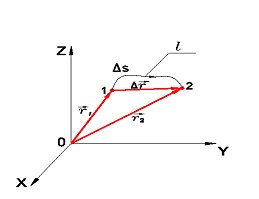
Проведем вектор  из начального положения материальной точки (поз.1) в её конечное положение- (поз.2). Вектор
из начального положения материальной точки (поз.1) в её конечное положение- (поз.2). Вектор  является геометрической разностью векторов
является геометрической разностью векторов  и
и  и представляет собой изменение радиуса-вектора, определяющего положение материальной точки за промежуток времени Δt = t2-t1, т.е. приращение функции
и представляет собой изменение радиуса-вектора, определяющего положение материальной точки за промежуток времени Δt = t2-t1, т.е. приращение функции  .
.
 .
.
Перемещением материальной точки (тела) называется вектор, проведённый из начального положения материальной точки в конечное.
Очевидно, что модуль вектора перемещения - это кратчайшее расстояние между начальным и конечным положениями материальной точки. Перемещение характеризует изменение положения тела интегрально (суммарно). Оно не показывает каким образом происходил этот процесс. Например, переместиться с Курского вокзала Москвы на Киевский можно либо по радиальной линии метро, либо по кольцевой, при этом вектор перемещения останется неизменным. Информацию о том, как фактически двигалось тело, дает нам траектория движения l , (рис.1.1)
Траекторией называется воображаемая или видимая линия, которую описывает в пространстве движущаяся материальная точка.
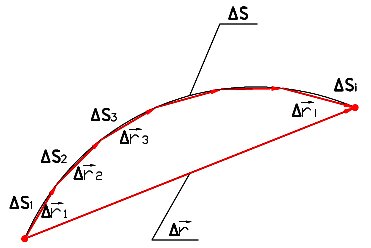
Примерами видимых траекторий являются: след от карандаша на чертеже, лыжня, следы метеоров, осветительных ракет, трассирующих пуль, железнодорожный путь и т.п. Форма траектории может быть произвольной: пространственная кривая, прямая или ломаная линия, окружность и т.д. Двигаясь по траектории из пункта 1 в пункт 2, (рис.1.1), материальная точка преодолевает расстояние - Δs, носящее название - путь.
Путь - это расстояние, пройденное материальной точкой по траектории движения за данный промежуток времени и равное длине этого участка траектории.
В отличие от перемещения - путь является скалярной положительной величиной. Любая траектория может быть разбита на отдельные элементарные участки. В случае, представленном на рис. 1.2, элементарными участками пути (Δs) являются длины дуг - Δs1, Δs2, ... Δsi, а векторы  , построенные на стягивающих эти дуги хордах представляют собой ряд последовательных перемещений. При этом суммарное перемещение
, построенные на стягивающих эти дуги хордах представляют собой ряд последовательных перемещений. При этом суммарное перемещение  равно геометрической сумме элементарных перемещений, а путь Δs, пройденный материальной точкой, равен арифметической сумме элементарных участков пути.
равно геометрической сумме элементарных перемещений, а путь Δs, пройденный материальной точкой, равен арифметической сумме элементарных участков пути.


Очевидно, что при непрямолинейном движении, модуль вектора перемещения -  всегда меньше величины пройденного пути - Δs, и, только при движении по прямой, эти величины равны.
всегда меньше величины пройденного пути - Δs, и, только при движении по прямой, эти величины равны.