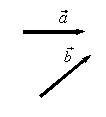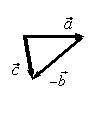Краткий справочник. Основные понятия кинематики

Материал из PhysBook

Перейти к: навигация, поиск

Материя. Пространство и время

Механическим движением тела называется изменение его положения в пространстве относительно других тел с течением времени.

Простейшими видами механического движения абсолютного твердого тела является поступательное и вращательное движение.

Признак поступательного движения:

тело движется поступательно, если при этом любая прямая, соединяющая две произвольные точки (А и В) тела, перемещается, оставаясь параллельной самой себе (рис. 1).

Рис. 1

При вращательном движении тела его точки описывают окружности, расположенные в параллельных плоскостях.

Тело можно принять за материальную точку, если:

тело движется поступательно;
размеры тела много меньше расстояния, которое оно проходит;
размеры тела много меньше расстояния до тела отсчета.

Путь – это длина участка траектории, пройденного точкой за данный промежуток времени.

Перемещение – направленный отрезок прямой, соединяющий начальное положение тела с его последующим положением.

Действия над векторами

Для того, чтобы построить вектор $~\vec c = \vec a + \vec b$ (рис. 2 а), воспользуемся правилами сложения векторов:

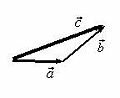
а) правило треугольника (рис. 2 б);

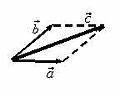
б) правило параллелограмма (рис. 2 в).

Для того, чтобы построить вектор $~\vec c = \vec a - \vec b$ (рис. 2 а), надо к вектору $~\vec a$ прибавить вектор $~-\vec b$ (рис. 2 г).

Рис. 2

Проекцией точки А на ось 0Х называется точка А₁, которая является основанием перпендикуляра АА₁, опущенного из точки А на ось 0Х (рис. 3).

Рис. 3

Проекция вектора $~\vec a$ на ось 0Х обозначается а_x, на ось 0Y – а_y.

Проекцией вектора $~\vec a$ на ось называется отрезок, заключенный между проекциями начала и конца вектора на данную ось (рис. 4).

Рис. 4

Проекция вектора на ось 0Х положительна, если координата конца вектора х больше координаты начала вектора х₀ (рис. 5 а), и отрицательна – если наоборот (рис. 5 б). Если вектор перпендикулярен оси, то его проекция равна нулю.

Рис. 5

Составляющей вектора $~\vec a$ по координатной оси 0Х называется вектор $~\vec a_x$ , начало которого совпадает с проекцией начала вектора $~\vec a$ на ось 0Х, а конец – с проекцией конца вектора. Аналогично для составляющей вектора $~\vec a$ на ось 0Y (рис. 6). Тогда проекция вектора положительна, если составляющая вектора на данную ось направлена вдоль выбранной оси (составляющая вектора $~\vec a_x$ ), и отрицательна – против оси (составляющая вектора $~\vec a_y$ ). Если вектор перпендикулярен оси, то его проекция равна нулю.

На рис. 6 проекция а_x > 0, а_y < 0.

Рис. 6

Δr_x = x – х₀; Δr_y = y – y₀,

где х₀, y₀ – координаты начала вектора $~\Delta \vec r$ (м); x, y – координаты конца вектора $~\Delta \vec r$ (м); Δr_x, Δr_y – проекции вектора $~\Delta \vec r$ на оси 0X и 0Y (м) (рис. 7).