КС. Твердые тела

Фазовые превращения

\(~Q = m \cdot \lambda \) ,

где Q – количество теплоты, которое необходимо сообщить телу для его плавления, или которое выделится при кристаллизации, если тело взято при температуре плавления (Дж); m – масса тела (кг); λ – удельная теплота плавления, табличная величина (Дж/кг).

• Количество теплоты будем считать положительным (Q > 0), если тепло подводим к телу, т.е. тело плавится.
• Количество теплоты будем считать отрицательным (Q < 0), если тело отдает тепло, т.е. тело кристаллизуется.
• Не ищите в таблицах температуру кристаллизации или удельную теплоту кристаллизации жидкости (например, воды) – вам надо таблица с температурой плавления или с удельной теплотой плавления данного вещества в твердом состоянии (для нашего примера – это лед), т.к. температуры плавления и удельная теплота плавления совпадает с температурой кристаллизации и удельной теплотой кристаллизации данных веществ.

Если температура тела не равна температуре плавления тела, то для того, чтобы тело расплавить (кристаллизовать), его вначале необходимо нагреть (охладить) до температуры плавления.

Рекомендации по решению задач

При нагревании (охлаждении) вещества от температуры t₁ до температуры t₂, вещество может менять свое агрегатное состояние. В этом случае необходимо рассматривать несколько процессов.

Чтобы определить какие процессы будут происходить и сколько их, найдем температуру плавления t_пл и температуру кипения t_кип данного вещества из табличных данных.

При нагревании тел от t₁ до t₂

1. Если t₁ < t_пл < t₂ < t_кип, то тело меняет свое агрегатное состояние: из твердого в жидкое. В этом случае происходит три процесса: 1) нагревание твердого тела; 2) плавление; 3) нагревание жидкости.
2. Если t_пл < t₁ < t_кип < t₂, то тело меняет свое агрегатное состояние: из жидкого в газообразное (пар). В этом случае происходит три процесса: 1) нагревание жидкости; 2) кипение; 3) нагревание газа (пара).
3. Если t₁ < t_пл < t_кип < t₂, то тело меняет свое агрегатное состояние дважды: из твердого в жидкое и из жидкого в газообразное (пар). В этом случае происходит пять процессов: 1) нагревание твердого тела; 2) плавление; 3) нагревание жидкости; 4) кипение; 5) нагревание газа (пара).

Анализ условия задач

План анализа условия задач, в которых возможны фазовые переходы, но неизвестна конечная температура системы:

• Определим, достаточно ли энергии, чтобы начался фазовый переход, который может быть при нагревании или охлаждении данного вещества.
• Определим, достаточно ли энергии, чтобы полностью произошел фазовый переход, который может быть при дальнейшем нагревании или охлаждении данного вещества.
• Определим, достаточно ли энергии, чтобы начался следующий фазовый переход, который может быть при нагревании или охлаждении данного вещества.

  и т.д.

Деформация

Вид деформации	Признаки
Растяжения	увеличивается расстояние между молекулярными слоями.
Сжатия	уменьшается расстояние между молекулярными слоями.
Кручения	поворот одних молекулярных слоев относительно других.
Изгиба	одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых.
Сдвига	одни слои молекул сдвигаются относительно других.
Упругая	после прекращения воздействия тело полностью восстанавливает первоначальную форму и размеры.
Пластичная	после прекращения воздействия тело не восстанавливает первоначальную форму или размеры.

Сила упругости

\(~\Delta l = |l - l_0|\) ,

где Δl – абсолютное удлинение (м); l и l₀ – конечная и начальная длина тела (м).

• Если тело растягивают, то l > l₀ и Δl = l – l₀;
• если тело сжимают, то l < l₀ и Δl = –(l – l₀) = l₀ – l.

\(~\varepsilon = \frac{\Delta l}{l_0}\) или \(~\varepsilon = \frac{\Delta l}{l_0} \cdot 100%\) ,

где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l₀ –начальная длина тела (м).

\(~\sigma = \frac{F_{upr}}{S}\) ,

где σ – механическое напряжение в деформированном теле (Па); F_upr – модуль силы упругости, возникающей в теле при деформации (Н); S – площадь поперечного сечения тела (м²).

\(~\sigma = E \varepsilon\) ,

где σ – механическое напряжение (Па); Е – модуль Юнга (модуль упругости), табличная величина (Па); ε – относительное удлинение (%).

\(~F_{upr} = k \Delta l\) ,

где F_upr – модуль силы упругости, возникающей в теле при деформации (Н); k – коэффициент жесткости (жесткость) тела (Н/м); Δl – абсолютное удлинение тела (м).

\(~\sigma_{pr} = \frac{F_{max}}{S}\) ,

где σ_pr – предел прочности (Па); F_max – максимальная сила, которую может выдержать тело, не разрушаясь (Н); S – площадь поперечного сечения тела (м²).

• При одномерных (линейных) деформациях растяжения или сжатия силы упругости направлены вдоль линии действия внешней (деформирующей) силы, т.е. вдоль осей продольно деформируемых нитей, витых пружин, стержней и т.п., или перпендикулярно к поверхностям соприкасающихся тел.

• Функция вида у = k·х – линейная, график такой функции прямая линия, проходящая через начало координат. Уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения F_upr = k·Δl. Это так же линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.

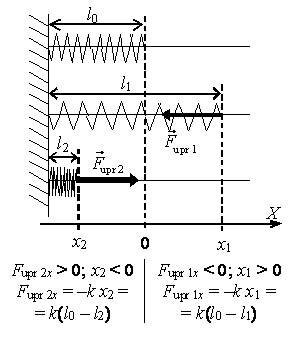
• Если ось 0Х направить вдоль тела в сторону его растяжения, начало отсчета выбрать в точке, совпадающей с концом недеформированного тела (рис. 1), то закон Гука можно записать так:

(F_upr)_x = –k·х ,

где (F_upr)_x – проекция сила упругости на ось 0Х (Н); х – координата конца тела.

• Знак «–» указывает, что сила упругости всегда противоположна по направлению абсолютному удлинению.

Рис. 1