КС. Силы в механике

Материал из PhysBook

Перейти к: навигация, поиск

Содержание

1 Сила упругости
2 Всемирное тяготение
3 Сила трения
4 Движение под действием нескольких сил

Сила упругости

Вид деформации	Признаки
Растяжения	увеличивается расстояние между молекулярными слоями.
Сжатия	уменьшается расстояние между молекулярными слоями.
Кручения	поворот одних молекулярных слоев относительно других.
Изгиба	одни молекулярные слои растягиваются, а другие сжимаются или растягиваются, но меньше первых.
Сдвига	одни слои молекул сдвигаются относительно других.
Упругая	после прекращения воздействия тело полностью восстанавливает первоначальную форму и размеры.
Пластичная	после прекращения воздействия тело не восстанавливает первоначальную форму или размеры.

$~\Delta l = |l - l_0|$ ,

где Δl – абсолютное удлинение (м); l и l₀ – конечная и начальная длина тела (м).

Если тело растягивают, то l > l₀ и Δl = l – l₀;
если тело сжимают, то l < l₀ и Δl = –(l – l₀) = l₀ – l.

$~\varepsilon = \frac{\Delta l}{l_0}$ или $~\varepsilon = \frac{\Delta l}{l_0} \cdot 100%$ ,

где ε – относительное удлинение тела (%); Δl – абсолютное удлинение тела (м); l₀ –начальная длина тела (м).

$~\sigma = \frac{F_{upr}}{S}$ ,

где σ – механическое напряжение в деформированном теле (Па); F_upr – модуль силы упругости, возникающей в теле при деформации (Н); S – площадь поперечного сечения тела (м²).

$~\sigma = E \varepsilon$ ,

где σ – механическое напряжение (Па); Е – модуль Юнга (модуль упругости), табличная величина (Па); ε – относительное удлинение (%).

$~F_{upr} = k \Delta l$ ,

где F_upr – модуль силы упругости, возникающей в теле при деформации (Н); k – коэффициент жесткости (жесткость) тела (Н/м); Δl – абсолютное удлинение тела (м).

$~\sigma_{pr} = \frac{F_{max}}{S}$ ,

где σ_pr – предел прочности (Па); F_max – максимальная сила, которую может выдержать тело, не разрушаясь (Н); S – площадь поперечного сечения тела (м²).

При одномерных (линейных) деформациях растяжения или сжатия силы упругости направлены вдоль линии действия внешней (деформирующей) силы, т.е. вдоль осей продольно деформируемых нитей, витых пружин, стержней и т.п., или перпендикулярно к поверхностям соприкасающихся тел.

Функция вида у = k·х – линейная, график такой функции прямая линия, проходящая через начало координат. Уравнение зависимости силы упругости, возникающей в деформированной пружине, от ее удлинения F_upr = k·Δl. Это так же линейная функция, проходящая через начало координат. Для построения такой прямой достаточно одной точки.

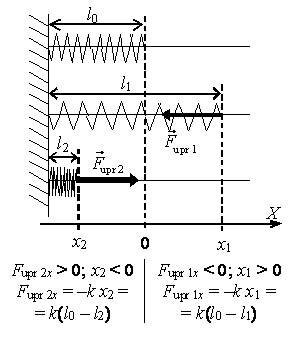
Если ось 0Х направить вдоль тела в сторону его растяжения, начало отсчета выбрать в точке, совпадающей с концом недеформированного тела (рис. 1), то закон Гука можно записать так:

$~(F_{upr})_x = - k \cdot x$ ,

где (F_upr)_x – проекция сила упругости на ось 0Х (Н); х – координата конца тела.

Знак «–» указывает, что сила упругости всегда противоположна по направлению абсолютному удлинению.

Рис. 1

Всемирное тяготение

$~F = G \cdot \frac{m_1 m_2}{r^2}$ ,

где F – сила всемирного тяготения (Н); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; m₁ и m₂ – массы взаимодействующих тел (кг); r – расстояние между телами (м).

Математические правила

х·10^a · y·10^b = x·y·10^a+b; х·10^a / (y·10^b) = x/y·10^a-b ; (x·10^a)ⁿ = xⁿ·10^an.

Например: 1,2·10^-11·(5·10¹⁰)² / (4·10¹⁵) = 1,2·(5)²/4 ·10^{-11 + 10·2 – 15} = 7,5·10^-6.

$~F_t = m g_{pl}$ ,

где F_t – сила тяжести (Н); g_pl – ускорение свободного падения планеты, табличная величина (м/с²); m – масса тела (кг).

g ≈ 9,81 м/с² – ускорение свободного падения у поверхности Земли.

$~F_t = G \cdot \frac{M_{pl} m}{r^2}$ ,

где F_t – сила тяжести (сила притяжения) на планете (Н); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); m – масса тела (кг); r = R_pl + h – расстояние от центра планеты до тела (м); R_pl – радиус планеты, табличная величина (м); h – высота тела над поверхностью планеты (м) (рис. 2).

Рис. 2

$~g_{pl} = G \cdot \frac{M_{pl}}{r^2}$ ,

где g_pl – ускорение свободного падения планеты, табличная величина (м/с²); G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); r = R_pl + h – расстояние от центра планеты до тела (м); R_pl – радиус планеты, табличная величина (м); h – высота тела над поверхностью планеты (м) (рис. 2).

Вес Р – это сила, с которой тело, вследствие земного притяжения действует на опору или подвес, неподвижные относительно него.

Примеры направления силы Р показаны на рис. 3 а-г.

Рис. 3 $~P_y = m \cdot (g_y - a_y)$ ,

где Р_y – проекция веса тела на ось 0Y (Н); m – масса тела (кг); a_y – проекция ускорения тела на ось 0Y (м/с²); g_y – проекция ускорение свободного падения на ось 0Y (м/с²).

Если направить ось 0Y вниз, то вес тела будет равен:

а) P = m·(g – a) (рис. 4 а),

б) P = m·(g + a) (рис. 4 б),

в) –P = m·(g – a) (рис. 4 в), P = m·(a – g).

Если направить ось 0Y вверх, то вес тела будет равен:

г) P = m·(a – g) (рис. 4 г).

Рис. 4

При прямолинейном движении:

– направления ускорения и скорости совпадают если значение скорости увеличивается;

– ускорение и скорость направлены в противоположные стороны, если значение скорости уменьшается.

При движении по окружности центростремительное ускорение направлено к центру окружности и равно $~a_c = \frac{\upsilon^2}{R}$ .

$~\upsilon = \sqrt{G \cdot \frac{M_{pl}}{r}}$ ,

где υ – скорость ИС (м/с), G – гравитационная постоянная, равная 6,67·10^-11 Н·м²/кг² ; M_pl – масса планеты, табличная величина (кг); r = R_pl + h – расстояние от центра планеты до ИС (м); R_pl – радиус планеты, табличная величина (м); h – высота ИС над поверхностью планеты (м) (рис. 2).

Первая космическая скорость для данной планеты – это скорость, которую нужно сообщить спутнику, чтобы он двигался по круговой орбите вблизи поверхности планеты.

Сила трения

F_tr = F_{tr p} = F, если F ≤ F_{tr sk}; F_tr = F_{tr sk}, если F > F_{tr sk} ,

где F_tr – сила трения (Н); F_{tr p} – сила трения покоя (Н); F – сила, действующая на тело (рис. 5) (Н), F_{tr sk} – сила трения скольжения (Н).

Рис. 5

$~F_{tr sk} = \mu N$ ,

где F_{tr sk} – сила трения скольжения (Н); μ – коэффициент трения скольжения, табличная величина; N = P = F_davl – сила реакции опоры (Н); Р – вес тела (Н); F_davl – сила нормального давления (Н).

Уравнение второго закона Ньютона в векторной форме имеет вид $~m \vec a = \vec F_1 + \vec F_2 + \vec F_3 + \ldots$
Проекция вектора

– положительна, если составляющая вектора на данную ось направлена вдоль этой оси;

– отрицательна – если против оси;

– равна нулю – если вектор перпендикулярен оси.

При изображении сил, не забывайте, что равнодействующая сил должна быть направлена в сторону ускорения.

Движение под действием нескольких сил

Задачи, в которых на тело действуют несколько сил, решайте, придерживаясь следующего плана решения задач:
1. Сделайте чертеж. Укажите все действующие на тело силы, укажите направления скорости и ускорения. Изобразите оси координат.
2. Запишите второй закон Ньютона в векторном виде и в проекциях на оси координат:
  
  $~m \vec a = \vec F_1 + \vec F_2 + \vec F_3 + \ldots$ ,
  
  OX: $~m a_x = F_{1x} + F_{2x} + F_{3x} + \ldots$ ,
  
  OY: $~m a_y = F_{1y} + F_{2y} + F_{3y} + \ldots$
  
  Определите значения проекций всех величин.
3. Решите полученные уравнения. При необходимости, исходя из физической природы, выразите силы через величины, от которых они зависят.

Если тело материальная точка, то его можно изобразить в виде прямоугольника или окружности, а все силы – выходящими из его центра;
если тело нельзя представить в виде материальной точки, то изображайте его, сохраняя форму, а силы изображайте с учетом точек их приложения.
При решении задач на движение тел под действием силы трения, часто необходимо использовать кинематические формулы.
При прямолинейном движении ускорение при торможении направлено против скорости;
при остановке конечная скорость равна нулю.
При равномерном движении по окружности тело движется с центростремительным ускорением, направленным к центру окружности и равным $~a_c = \frac{\upsilon^2}{R} = \omega^2 R$ .
Если в условии задачи говорится о системе материальных тел, то необходимо записывать уравнение второго закона Ньютона для каждого тела системы в отдельности.
Можно выбирать разные системы координат для разных тел.
Систему, изображенную на рис. 6 а, называют коническим маятником; на рис. 6 б – математическим маятником.

Рис. 6

Скорость конического маятника не меняется по величине, поэтому ускорение груза равно центростремительному ускорению, направленному к центру окружности.
Скорость математического маятника изменяется по величине, поэтому ускорение груза $~a = \sqrt{a^2_c + a^2_{\tau}}$ , где а_c – центростремительное ускорение, направленное к центру окружности (вдоль подвеса); а_τ – тангенциальное ускорение, направленное также как и скорость (по касательной), если скорость увеличивается, и в противоположную сторону, если скорость уменьшается.
Если тело находится в системе, которая движется с ускорением, то можно применять несколько способ решения задач:

1 способ. Второй закон Ньютона записать в следующем виде: $~m \vec a_t = \vec F_1 + \vec F_2 + \ldots$ , где $~\vec a_t = \vec a_c + \vec a_{t/c}$ – ускорение тела относительно неподвижной системы (Земли), $~\vec a_c$ – ускорение системы, в которой находится тело, $~\vec a_{t/c}$ – ускорение тела относительно движущейся системы.

2 способ. Перейти в НИСО, тогда второй закон Ньютона будет иметь вид $~m \vec a_{t/c} = \vec F_{in} + \vec F_1 + \vec F_2 + \ldots$ , где $~\vec a_{t/c}$ – ускорение тела относительно движущейся системы, $~\vec F_{in}$ – сила инерции, которая направлена против ускорения системы а_c, а по величине равна F_in = m∙а_c, $~\vec a_c$ – ускорение системы.

Смотреть HD

видео онлайн

бесплатно 2022 года

Источник — «http://www.physbook.ru/index.php/%D0%9A%D0%A1._%D0%A1%D0%B8%D0%BB%D1%8B_%D0%B2_%D0%BC%D0%B5%D1%85%D0%B0%D0%BD%D0%B8%D0%BA%D0%B5»