КС. Равноускоренное движение

Равноускоренное движение

Равноускоренное прямолинейное движение — это движение, при котором скорость тела за любые равные промежутки времени изменяется одинаково, т.е. это движение с постоянным по модулю и направлению ускорением.

Движение будет равноускоренным и если скорость увеличивается, и если скорость уменьшается. Хотя некоторые авторы задач движение тел с уменьшающей скоростью называют равнозамедленным движением.

Ускорение тела при равноускоренном движении называется величина, равная отношению изменения скорости тела $~\Delta \vec{\upsilon }=\vec{\upsilon }-\vec{\upsilon }_{0}$ к промежутку времени t, в течение которого это изменение произошло, т.е.

$~\vec{a}=\dfrac{\vec{\upsilon }-\vec{\upsilon }_{0} }{t}$ или в проекции на ось 0X $$~a_{x} =\dfrac{\upsilon _{x} -\upsilon _{0x} }{t} .$$

• Обозначается буквой а, измеряется в метрах за секунду в квадрате (м/с²).

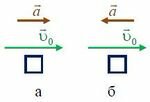
При прямолинейном движении ускорение $~\vec{a}$ направлено:

• в сторону движения (скорости), если скорость тела увеличивается (рис. 1, а);
• в противоположную сторону движения (скорости), если скорость тела уменьшается (рис. 1, б).

Рис. 1

И наоборот:

• если направления ускорения $~\vec{a}$ и движения (скорости) совпадают, то скорость тела увеличивается (см. рис. 1, а);
• если ускорение $~\vec{a}$ направлено в противоположную сторону движения (скорости), то скорость тела уменьшается (см. рис. 1, б).

При решении задач на равноускоренное движение чаще всего используют два уравнения

$~\upsilon _{x} =\upsilon _{0x} +a_{x} \cdot t, \;\;\; \Delta r_{x} =\upsilon _{0x} \cdot t+\dfrac{a_{x} \cdot t^{2} }{2} ,$

где υ_x — проекция конечной скорости на ось 0Х (м/с), υ_0x — проекция начальной скорости на ось 0Х (м/с), Δr_x — проекция перемещения на ось 0Х (м), а_х — проекция ускорения на ось 0Х (м/с²), t — время, в течение которого изменяется скорость (с).

Таблица уравнений

Но задачу на равноускоренное движение можно решить быстрее, если вы запомните пять уравнений (таблица 1).

Таблица 1

№	Формула	Используемые величины	Отсутствующие величины
1	$~\Delta r_x = \upsilon_{0x} \cdot t + \dfrac{a_x \cdot t^2}{2}$	Δrx, υ0x, ax и t	υx
2	$~\Delta r_x = \upsilon_x \cdot t - \dfrac{a_x \cdot t^2}{2}$	Δrx, υx, ax и t	υ0x
3	$~\Delta r_x = \dfrac{\upsilon^2_x - \upsilon^2_{0x}}{2 a_x}$	Δrx, υ0x, υx и ax	t
4	$~\Delta r_x = \dfrac{\upsilon_x + \upsilon_{0x}}{2} \cdot t$	Δrx, υ0x, υx и t	ax
5	$~\upsilon_x = \upsilon_{0x} + a_x \cdot t$	υ0x, υx, ax и t	Δrx

В уравнениях (1) - (5) используются пять величин: проекции перемещения Δr_x, проекции начальной скорости υ_0x, проекции конечной скорости υ_x, проекции ускорения a_x и времени t (см. таблицу 1). По этим величинам можно определить, какой формулой лучше всего пользоваться. Например, если требуется найти перемещение Δr_x, а известны υ_x, υ_0x и a_x, то можно воспользоваться формулой (3), т.к. отсутствует время t.

Уравнения (2) - (4) можно получить из уравнений (1) и (5), но на это требуется время. Например, по условию даны значения проекций скоростей υ_0x, υ_x и ускорения a_x, найти перемещение Δr_x. Вы можете сразу применить уравнение (3) (если вы его запомнили), или вначале выразить время t из уравнения (5) и подставить его в уравнение (1):

$ $$\begin{array}{c} {t=\dfrac{\upsilon _{x} -\upsilon _{0x} }{a_{x} } ,\; \; \; \Delta r_{x} =\upsilon _{0x} \cdot t+\dfrac{a_{x} \cdot t^{2} }{2} =\upsilon _{0x} \cdot \dfrac{\upsilon _{x} -\upsilon _{0x} }{a_{x} } +\dfrac{a_{x} }{2} \cdot \left(\dfrac{\upsilon _{x} -\upsilon _{0x} }{a_{x} } \right)^{2} =\dfrac{\upsilon _{0x} \cdot \upsilon _{x} -\upsilon _{0x}^{2} }{a_{x} } +} \\ {+\dfrac{\upsilon _{x}^{2} -2\upsilon _{x} \cdot \upsilon _{0x} +\upsilon _{0x}^{2} }{2a_{x} } =\dfrac{2\upsilon _{0x} \cdot \upsilon _{x} -2\upsilon _{0x}^{2} +\upsilon _{x}^{2} -2\upsilon _{x} \cdot \upsilon _{0x} +\upsilon _{0x}^{2} }{2a_{x} } =\dfrac{\upsilon _{x}^{2} -\upsilon _{0x}^{2} }{2a_{x} } .} \end{array}$$ $

Аналогично можно получить уравнения (2) и (4). Выбирайте сами, что для вас проще: выводить формулы или их запомнить.