КС. Движение в пространстве

Тело брошено под углом к горизонту

Движение тела, брошенного под углом к горизонту, можно разложить на два движения:

• равномерное движение по горизонтали со скоростью υ_0x, и тогда для описания движения вдоль оси 0Х применяются формулы равномерного движения:

проекция скорости υ_x = υ_0x; уравнение движения x = x0 + υ_0x∙t;

• равноускоренное движение по вертикали с ускорением g и скоростью υ_y – для описания движения вдоль оси 0Y применяются формулы равноускоренного движения по вертикали:

проекция скорости υ_y = υ_0y + g_y·t; уравнение движения \(~y = y_0 + \upsilon_{0y} \cdot t + \frac{g_y \cdot t^2}{2}\) .

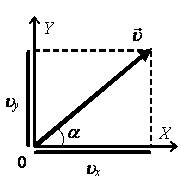
Скорость тела в любой момент времени будет равна (рис. 1)\[~\upsilon = \sqrt{\upsilon^2_x + \upsilon^2_y} ; \upsilon = \frac{\upsilon_x}{\cos \alpha} ; \upsilon = \frac{\upsilon_y}{\sin \alpha}\] или υ_x = υ cos α ; υ_y = υ sin α.

Рис. 1